Cho gia tốc rơi tự do trên mặt đất là go = 9,8 m/s^2. Tìm độ cao của vật có gia tốc rơi tự do là 8,9 m/s^2. Biết bán kính Trái Đất R = 6400 km
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.
F h d = F h t ⇔ G m M r 2 = m v 2 r ⇒ v = G M r
Với: r = R + h = R + R = 2 R
Nên: v = G M 2 R
Mặt khác:
Gia tốc rơi tự do của vật ở mặt đất: g = G M R 2 ⇒ G M = g R 2
⇒ v = g R 2 2 R = g R 2 = 9 , 8.6400000 2 = 5600 m / s = 5 , 6 km / s
Đáp án: D

Ta có
+ Công thức tính gia tốc trọng trường tại bề mặt Trái Đất g = GM/ R 2
+ Công thức tính gia tốc trọng trường tại độ cao h so với bề mặt Trái Đất g' = GM/ R + h 2
Suy ra g' = g R / R + h 2
a. h = 3200 m = 3,2 km
g' = 9,8. 6400 / 6403 , 2 2 = 9,79(m/ s 2 )
b. h = 3200 km
g' = 9,8. 6400 / 9600 2 = 4,35(m/ s 2 )

Áp dụng công thức:
\(g=g_0.\dfrac{R^2}{(R+h)^2}\)
Trong đó, \(g_0\) là gia tốc trọng trường ở mặt đất.
$R$ là bán kính trái đất.
$h$ là độ cao của vật.

Tại mặt đất: \(g_0=G\cdot\dfrac{M}{R^2}\)
Tại độ cao h: \(g=G\cdot\dfrac{M}{\left(R+h\right)^2}\)
Xét tỉ lệ:
\(\dfrac{g_0}{g}=\dfrac{\left(R+h\right)^2}{R^2}=\dfrac{9,81}{4,9}=2\)
\(\Rightarrow\dfrac{\left(R+h\right)^2}{R^2}=2\Rightarrow h=2650,97km\)
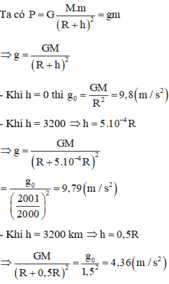
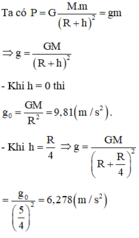

Khi ở trên mặt đất => \(h< < R\) => bỏ qua h
\(g=\frac{GM}{R^2}\Leftrightarrow GM=g.R^2=9,8.R^2\)
Khi rơi ở độ cao h
\(g=\frac{GM}{\left(R+h\right)^2}\Leftrightarrow8,9=\frac{9,8.6400000^2}{\left(6400000+h\right)^2}\)
=> h= ...(tự tính nha)