\(x-\sqrt{x+3}+1=0\)\(0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
a.
$x^2-11=0$
$\Leftrightarrow x^2=11$
$\Leftrightarrow x=\pm \sqrt{11}$
b. $x^2-12x+52=0$
$\Leftrightarrow (x^2-12x+36)+16=0$
$\Leftrightarrow (x-6)^2=-16< 0$ (vô lý)
Vậy pt vô nghiệm.
c.
$x^2-3x-28=0$
$\Leftrightarrow x^2+4x-7x-28=0$
$\Leftrightarrow x(x+4)-7(x+4)=0$
$\Leftrightarrow (x+4)(x-7)=0$
$\Leftrightarrow x+4=0$ hoặc $x-7=0$
$\Leftrightarrow x=-4$ hoặc $x=7$
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
d.
$x^2-11x+38=0$
$\Leftrightarrow (x^2-11x+5,5^2)+7,75=0$
$\Leftrightarrow (x-5,5)^2=-7,75< 0$ (vô lý)
Vậy pt vô nghiệm
e.
$6x^2+71x+175=0$
$\Leftrightarrow 6x^2+21x+50x+175=0$
$\Leftrightarrow 3x(2x+7)+25(2x+7)=0$
$\Leftrightarrow (3x+25)(2x+7)=0$
$\Leftrightarrow 3x+25=0$ hoặc $2x+7=0$
$\Leftrightarrow x=-\frac{25}{3}$ hoặc $x=-\frac{7}{2}$
18 tháng 10 2021
\(Q=\dfrac{\sqrt{x}-3-\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{x-1-x+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\\ Q=\dfrac{-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{8}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\\ Q=\dfrac{-6\sqrt{x}+1+8\sqrt{x}+24}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\\ Q=\dfrac{2\sqrt{x}+25}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
H9
HT.Phong (9A5)
CTVHS
1 tháng 8 2023
a) \(A=\dfrac{x\sqrt{y}+y\sqrt{x}}{x+2\sqrt{xy}+y}\)
\(A=\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)^2}\)
\(A=\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
b) \(B=\dfrac{x\sqrt{y}-y\sqrt{x}}{x-2\sqrt{xy}+y}\)
\(B=\dfrac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)^2}\)
\(B=\dfrac{\sqrt{xy}}{\sqrt{x}-\sqrt{y}}\)
c) \(C=\dfrac{3\sqrt{a}-2a-1}{4a-4\sqrt{a}+1}\)
\(C=\dfrac{-\left(2a-3\sqrt{a}+1\right)}{\left(2\sqrt{a}\right)^2-2\sqrt{a}\cdot2\cdot1+1^2}\)
\(C=\dfrac{-\left(\sqrt{a}-1\right)\left(2\sqrt{a}-1\right)}{\left(2\sqrt{a}-1\right)^2}\)
\(C=\dfrac{-\sqrt{a}+1}{2\sqrt{a}-1}\)
d) \(D=\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\)
\(D=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{\sqrt{a}-2}\)
\(D=\sqrt{a}+2-\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}{\sqrt{a}-2}\)
\(D=\left(\sqrt{a}+2\right)-\left(\sqrt{a}+2\right)\)
\(D=0\)
15 tháng 7 2023
1) \(\sqrt[]{3x+7}-5< 0\)
\(\Leftrightarrow\sqrt[]{3x+7}< 5\)
\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)
\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)
\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)
11 tháng 9 2023
a: =>2sin(x+pi/3)=-1
=>sin(x+pi/3)=-1/2
=>x+pi/3=-pi/6+k2pi hoặc x+pi/3=7/6pi+k2pi
=>x=-1/2pi+k2pi hoặc x=2/3pi+k2pi
b: =>2sin(x-30 độ)=-1
=>sin(x-30 độ)=-1/2
=>x-30 độ=-30 độ+k*360 độ hoặc x-30 độ=180 độ+30 độ+k*360 độ
=>x=k*360 độ hoặc x=240 độ+k*360 độ
c: =>2sin(x-pi/6)=-căn 3
=>sin(x-pi/6)=-căn 3/2
=>x-pi/6=-pi/3+k2pi hoặc x-pi/6=4/3pi+k2pi
=>x=-1/6pi+k2pi hoặc x=3/2pi+k2pi
d: =>2sin(x+10 độ)=-căn 3
=>sin(x+10 độ)=-căn 3/2
=>x+10 độ=-60 độ+k*360 độ hoặc x+10 độ=240 độ+k*360 độ
=>x=-70 độ+k*360 độ hoặc x=230 độ+k*360 độ
e: \(\Leftrightarrow2\cdot sin\left(x-15^0\right)=-\sqrt{2}\)
=>\(sin\left(x-15^0\right)=-\dfrac{\sqrt{2}}{2}\)
=>x-15 độ=-45 độ+k*360 độ hoặc x-15 độ=225 độ+k*360 độ
=>x=-30 độ+k*360 độ hoặc x=240 độ+k*360 độ
f: \(\Leftrightarrow sin\left(x-\dfrac{pi}{3}\right)=-\dfrac{1}{\sqrt{2}}\)
=>x-pi/3=-pi/4+k2pi hoặc x-pi/3=5/4pi+k2pi
=>x=pi/12+k2pi hoặc x=19/12pi+k2pi
12 tháng 9 2023
g) \(3+\sqrt[]{5}sin\left(x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=-\dfrac{3}{\sqrt[]{5}}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=sin\left[arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)\right]\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)+k2\pi\\x+\dfrac{\pi}{3}=\pi-arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)-\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}-arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)+k2\pi\end{matrix}\right.\)
h) \(1+sin\left(x-30^o\right)=0\)
\(\Leftrightarrow sin\left(x-30^o\right)=-1\)
\(\Leftrightarrow sin\left(x-30^o\right)=sin\left(-90^o\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-30^o=-90^0+k360^o\\x-30^o=180^o+90^0+k360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-60^0+k360^o\\x=300^0+k360^o\end{matrix}\right.\)
\(\Leftrightarrow x=-60^0+k360^o\)
AH
Akai Haruma
Giáo viên
4 tháng 9 2021
1. ĐKXĐ: $x\geq 4$
PT $\Leftrightarrow \sqrt{x-1}=5-\sqrt{x-4}$
$\Rightarrow x-1=25+x-4-10\sqrt{x-4}$
$\Leftrightarrow 22=10\sqrt{x-4}$
$\Leftrightarrow 2,2=\sqrt{x-4}$
$\Leftrightarrow 4,84=x-4\Leftrightarrow x=8,84$
(thỏa mãn)
2. ĐKXĐ: $x\geq 0$
PT $\Leftrightarrow (2x-2\sqrt{x})-(5\sqrt{x}-5)=0$
$\Leftrightarrow 2\sqrt{x}(\sqrt{x}-1)-5(\sqrt{x}-1)=0$
$\Leftrightarrow (\sqrt{x}-1)(2\sqrt{x}-5)=0$
$\Leftrightarrow \sqrt{x}-1=0$ hoặc $2\sqrt{x}-5=0$
$\Leftrightarrow x=1$ hoặc $x=\frac{25}{4}$ (tm)
AH
Akai Haruma
Giáo viên
4 tháng 9 2021
3. ĐKXĐ: $x\geq 3$
Bình phương 2 vế thu được:
$3x-2+2\sqrt{(2x+1)(x-3)}=4x$
$\Leftrightarrow 2\sqrt{(2x+1)(x-3)}=x+2$
$\Leftrightarrow 4(2x+1)(x-3)=(x+2)^2$
$\Leftrightarrow 4(2x^2-5x-3)=x^2+4x+4$
$\Leftrightarrow 7x^2-24x-16=0$
$\Leftrightarrow (x-4)(7x+4)=0$
Do $x\geq 3$ nên $x=4$
Thử lại thấy thỏa mãn
Vậy $x=4$
8 tháng 7 2021
a) Ta có: \(\sqrt{49\left(x^2-2x+1\right)}-35=0\)
\(\Leftrightarrow7\left|x-1\right|=35\)
\(\Leftrightarrow\left|x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=5\\x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-4\end{matrix}\right.\)
b)
ĐKXĐ: \(\left[{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\)
Ta có: \(\sqrt{x^2-9}-5\sqrt{x+3}=0\)
\(\Leftrightarrow\sqrt{x+3}\left(\sqrt{x-3}-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+3}=0\\\sqrt{x-3}=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-3=25\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\left(nhận\right)\\x=28\left(nhận\right)\end{matrix}\right.\)
c) ĐKXĐ: \(x\ge0\)
Ta có: \(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=\dfrac{\sqrt{x}-1}{\sqrt{x}+3}\)
\(\Leftrightarrow x-1=x+\sqrt{x}-6\)
\(\Leftrightarrow\sqrt{x}-6=-1\)
\(\Leftrightarrow\sqrt{x}=5\)
hay x=25(nhận)
T
11 tháng 10 2023
\(a,A=\left(\dfrac{3\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}-3\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\left(đk:x\ge0;x\ne1\right)\)
\(=\left[\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right]\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{3x+3\sqrt{x}-\sqrt{x}+1-3\left(x-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{3x+2\sqrt{x}+1-3x+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2}{\sqrt{x}-1}\)
\(---\)
\(b,A< 0\Leftrightarrow\dfrac{2}{\sqrt{x}-1}< 0\)
\(\Leftrightarrow\sqrt{x}-1< 0\)
\(\Leftrightarrow\sqrt{x}< 1\)
\(\Leftrightarrow x< 1\)
Kết hợp với điều kiện của \(x\), ta được:
\(0\le x< 1\)
Vậy: ...
\(Toru\)
H9
HT.Phong (9A5)
CTVHS
11 tháng 10 2023
a) \(A=\left(\dfrac{3\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}-3\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(A=\left[\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+1\right)}\right]\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(A=\dfrac{3x+3\sqrt{x}-\sqrt{x}+1-3x+3}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(A=\dfrac{2\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(A=\dfrac{2\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(A=\dfrac{2}{\sqrt{x}-1}\)
b) \(A< 0\) khi
\(\dfrac{2}{\sqrt{x}-1}< 0\Leftrightarrow\sqrt{x}-1< 0\)
\(\Leftrightarrow\sqrt{x}< 1\)
\(\Leftrightarrow x< 1\)
Kết hợp với đk:
\(0\le x< 1\)
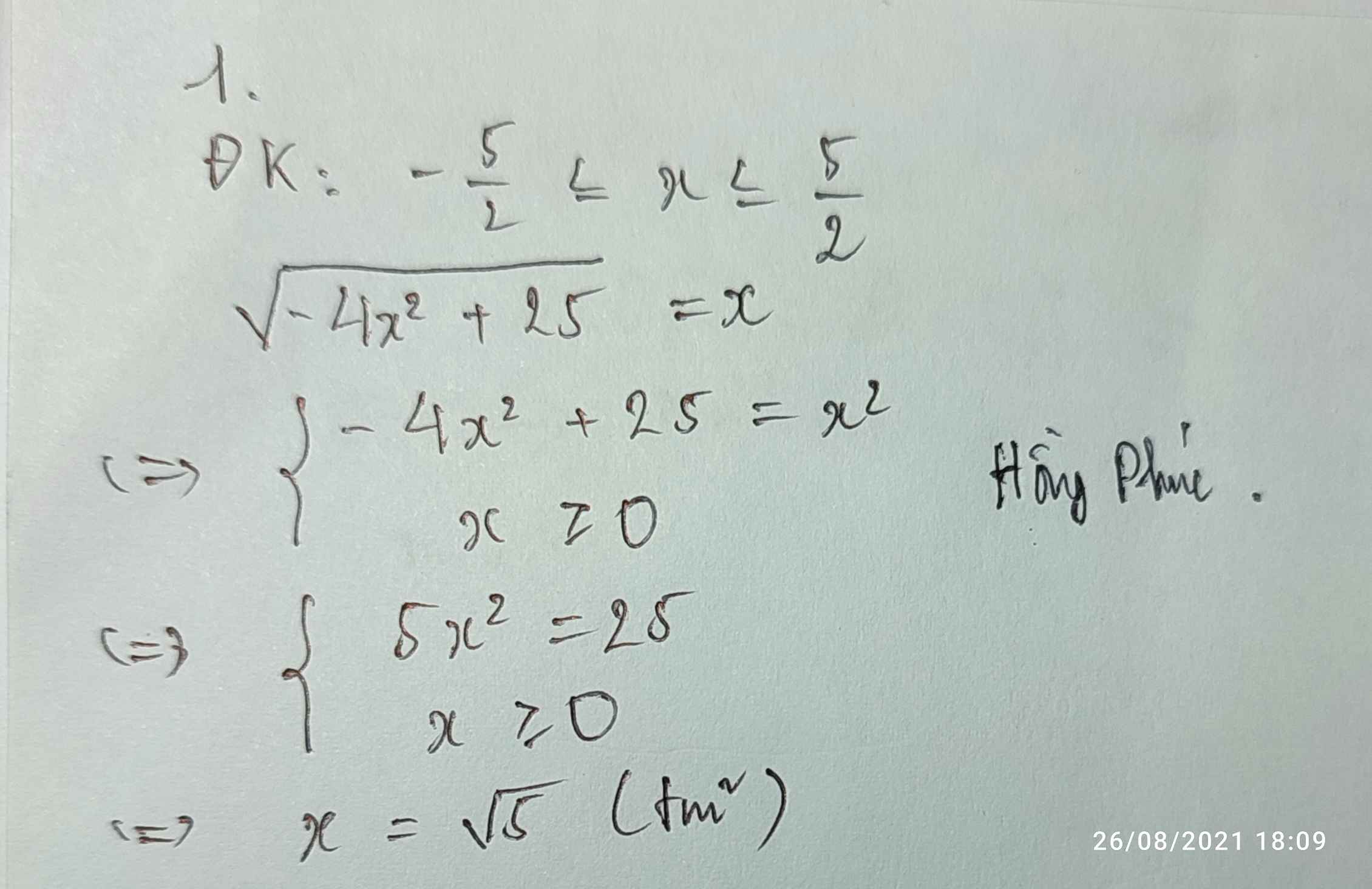
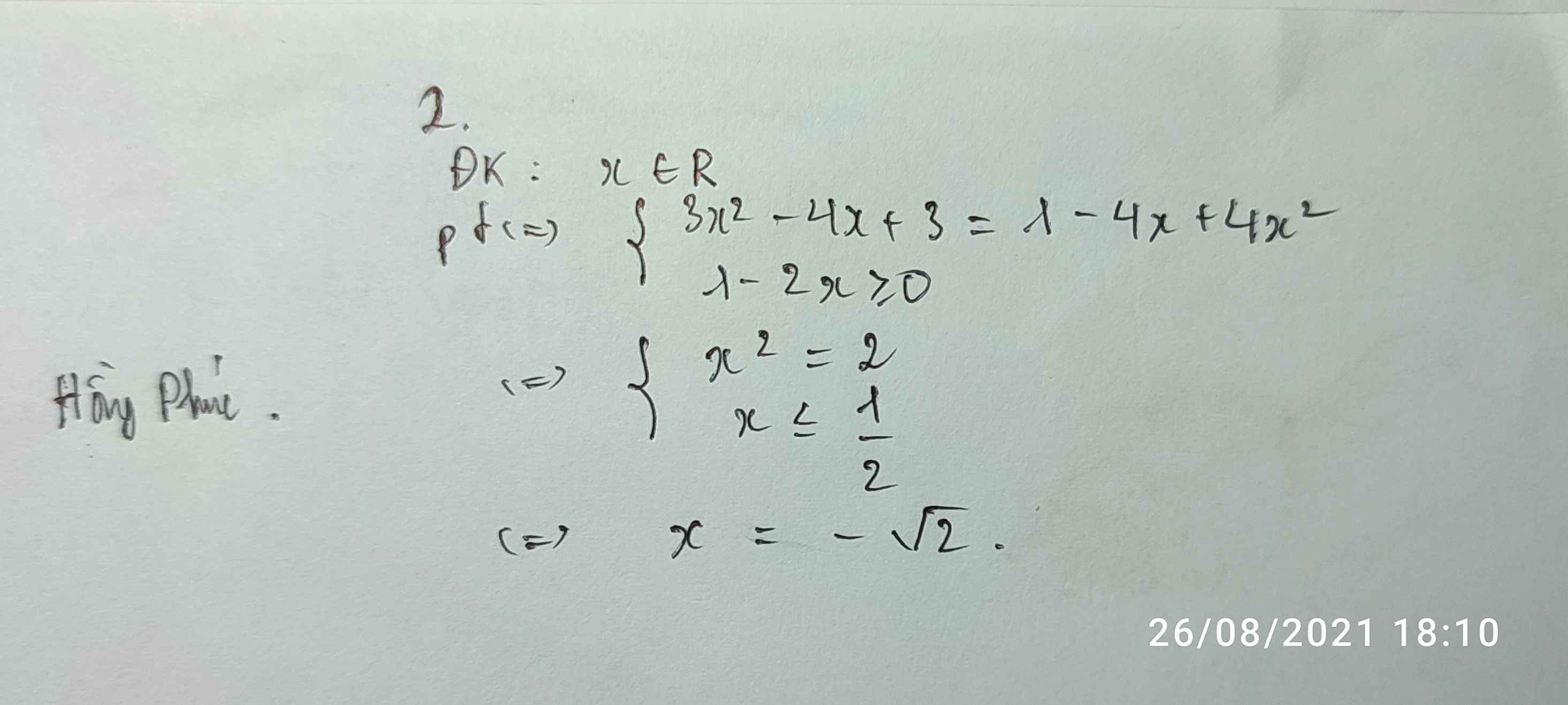
x-1=căn x+3
x^2-2x+1=x+3
x^2-3x-2=0
(x-1)(x-2)=0
x=1 hoặc x=2