Cho hàm số \(y=\left(5-2\sqrt{7}\right)x+1\)
a, Hàm số đồng biến hay nghịch biến trên R?
b, Tìm các giá trị của y tương ứng với các giá trị của x: 0; 1; \(\sqrt{7}\) ; \(5+2\sqrt{7}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 12 2023
Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)
24 tháng 10 2021
a, Vì \(5-3\sqrt{2}>0\) nên hs đồng biến trên R
b, \(x=5+3\sqrt{2}\Leftrightarrow y=25-18+\sqrt{2}-1=6+\sqrt{2}\)
c, \(y=0\Leftrightarrow\left(5-3\sqrt{2}\right)x+\sqrt{2}-1=0\Leftrightarrow x=\dfrac{1-\sqrt{2}}{5-3\sqrt{2}}\)
\(\Leftrightarrow x=\dfrac{\left(1-\sqrt{2}\right)\left(5+3\sqrt{2}\right)}{7}=\dfrac{-2\sqrt{2}-1}{7}\)
AH
Akai Haruma
Giáo viên
12 tháng 9 2021
Lời giải:
a. Vì $\sqrt{3}-1>0$ nên hàm trên là hàm đồng biến trên $\mathbb{R}$
b.
$F(0)=(\sqrt{3}-1).0+1=1$
$F(\sqrt{3}+1)=(\sqrt{3}-1)(\sqrt{3}+1)+1=(3-1)+1=3$
22 tháng 7 2021
a) Vì \(3-2\sqrt{2}>0\) nên hàm số đồng biến
b) Thay \(x=3+2\sqrt{2}\) vào hàm số, ta được:
\(y=\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)+\sqrt{2}-1\)
\(=9-8+\sqrt{2}-1\)
\(=\sqrt{2}\)
TA
22 tháng 7 2021
a) `a=3-2\sqrt2>0 =>` Hàm số đồng biến.
b) `y=(3-2\sqrt2)(3+2\sqrt2)+\sqrt2-1=3^2-(2\sqrt2)^2+\sqrt2-1=\sqrt2`
`=> y=\sqrt2` khi `x=3+2\sqrt2`
CM
25 tháng 4 2018
Ta có:
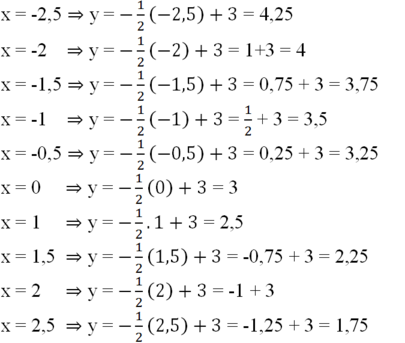
Ta được bảng sau:
b) Hàm số đã cho là hàm số nghịch biến trên R vì khi giá trị của biến x tăng lên mà giá trị tương ứng f(x) lại giảm đi.
24 tháng 2 2021
a) Để hàm số \(y=\left(\sqrt{2n+5}-2\right)x^2\) nghịch biến với mọi x<0 thì
\(\sqrt{2n+5}-2>0\)
\(\Leftrightarrow\sqrt{2n+5}>2\)
\(\Leftrightarrow2n+5>4\)
\(\Leftrightarrow2n>-1\)
\(\Leftrightarrow n>-\dfrac{1}{2}\)
Kết hợp ĐKXĐ, ta được: \(n>-\dfrac{1}{2}\)
Vậy: Để hàm số \(y=\left(\sqrt{2n+5}-2\right)x^2\) nghịch biến với mọi x<0 thì \(n>-\dfrac{1}{2}\)
b) Để hàm số \(y=\left(\sqrt{2n+5}-2\right)x^2\) đồng biến với mọi x<0 thì \(\sqrt{2n+5}-2< 0\)
\(\Leftrightarrow\sqrt{2n+5}< 2\)
\(\Leftrightarrow2n+5< 4\)
\(\Leftrightarrow2n< -1\)
\(\Leftrightarrow n< -\dfrac{1}{2}\)
Kết hợp ĐKXĐ, ta được: \(-\dfrac{5}{2}\le n< \dfrac{1}{2}\)
Vậy: Để hàm số \(y=\left(\sqrt{2n+5}-2\right)x^2\) đồng biến với mọi x<0 thì \(-\dfrac{5}{2}\le n< \dfrac{1}{2}\)
24 tháng 2 2021
a,Nghịch biến khi `x<0`
`<=>\sqrt{2n+5}-2>0(x>=-5/2)`
`<=>\sqrt{2n+5}>2`
`<=>2n+5>4`
`<=>2n> -1`
`<=>n> -1/2`
Kết hợp ĐKXĐ:
`=>n>1/2`
b,Đồng biến với mọi `x<0`
`<=>\sqrt{2n+5}-2<0`
`<=>\sqrt{2n+5}<2`
`<=>2n+5<4`
`<=>2n< -1`
`<=>n< -1/2`
Kết hợp ĐKXĐ:
`=>-5/2<x< -1/2`
12 tháng 11 2023
a: \(y=-x^3-3x^2+\left(5-m\right)x\)
=>\(y'=-3x^2-3\cdot2x+5-m\)
=>\(y'=-3x^2-6x+5-m\)
Để hàm số nghịch biến trên R thì \(y'< =0\forall x\)
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(-6\right)^2-4\cdot\left(-3\right)\left(5-m\right)< =0\\-3< 0\end{matrix}\right.\)
=>\(36+12\left(5-m\right)< =0\)
=>\(36+60-12m< =0\)
=>\(-12m+96< =0\)
=>-12m<=-96
=>m>=8
b: \(y=x^3+\left(2m-2\right)\cdot x^2+mx\)
=>\(y'=3x^2+2\left(2m-2\right)\cdot x+m\)
=>\(y'=3x^2+\left(4m-4\right)x+m\)
Để hàm số đồng biến trên R thì y'>=0 với mọi x
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3>0\\\left(4m-4\right)^2-4\cdot3\cdot m< =0\end{matrix}\right.\)
=>\(16m^2-32m+16-12m< =0\)
=>\(16m^2-44m+16< =0\)
=>\(4m^2-11m+4< =0\)
=>\(\dfrac{11-\sqrt{57}}{8}< =m< =\dfrac{11+\sqrt{57}}{8}\)
30 tháng 12 2023
Bài 1:
Để hàm số y=(2-m)x-2 là hàm số bậc nhất thì 2-m<>0
=>m<>2
a=2-m
b=-2
Bài 2:
a: Để hàm số y=(m-5)x+1 đồng biến trên R thì m-5>0
=>m>5
b: Để hàm số y=(m-5)x+1 nghịch biến trên R thì m-5<0
=>m<5
Bài 3:
a: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}3-m=2\\2\ne m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=1\)
b: Để (d1) cắt (d2) thì \(3-m\ne2\)
=>\(m\ne1\)
c: Để (d1) cắt (d2) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}3-m\ne2\\m=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\m=2\end{matrix}\right.\)
=>m=2