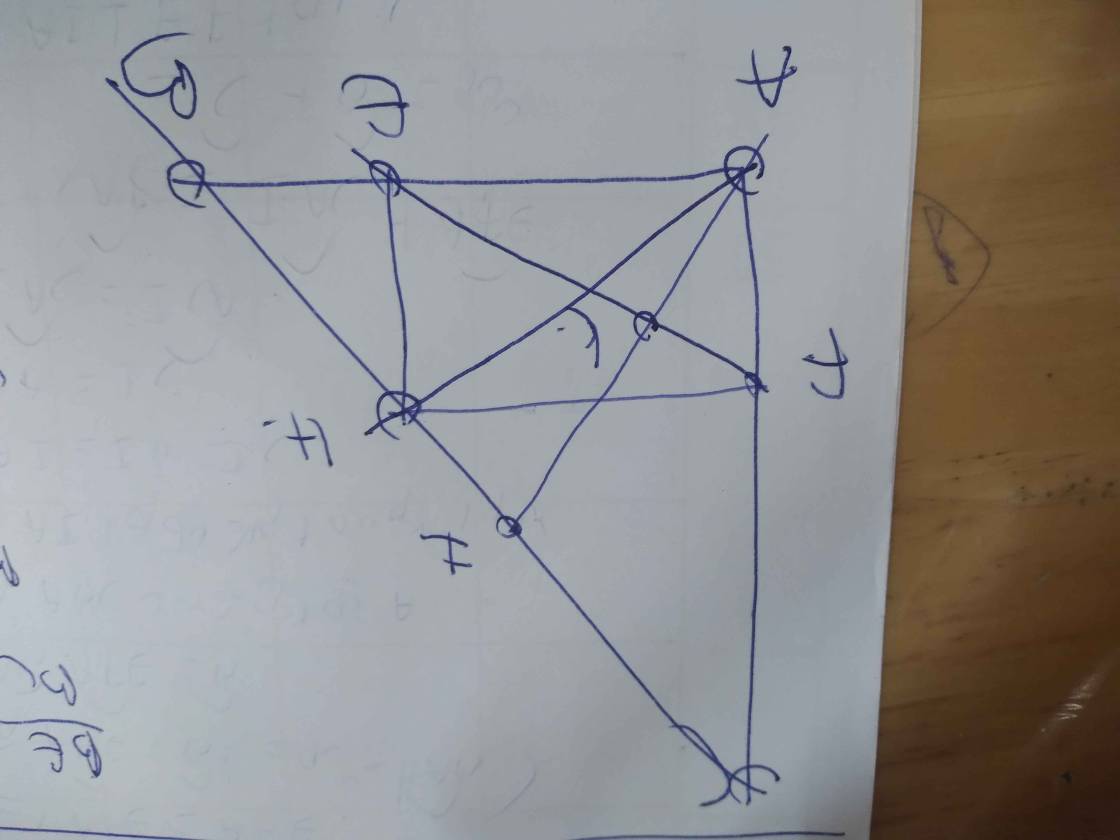
Cho ΔABC vuông tại A có đường cao AH
a, CMR : BC = AH . cotB + AH . cotC
b, Kẻ HE ⊥ AB
CMR : BE = BC . cos3B
c, Kẻ HF ⊥ AC
CMR : ΔAEF ~ ΔACB
d, CMR : \(\frac{BE}{CF}=\frac{AB^3}{AC^3}\)
e, \(\sqrt{\frac{BE}{AE}}=\frac{BH}{AH}\)
f, AH3 = BC . HE . HF
g, BE\(\sqrt{CH}\) + CF\(\sqrt{BH}\)= AH\(\sqrt{BC}\)
h, \(\sqrt[3]{BE^3}+\sqrt[3]{CF^3}=\sqrt[3]{BC^2}\)