cho hai đường tròn (O:R)và (O':R') tiếp xúc ngoài tại A(r>R').Vẽ dây AB của (O)và dây AC của (O') sao cho AB vuông góc với AC.
a)chứng minh OB//O'C.
b)chứng mkinh rằng khi B thay đổi trên (O) thì BC đi qua 1 điểm cố định.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

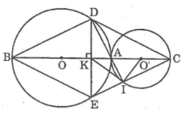
Tam giác DIE vuông tại I có IK là trung tuyến thuộc cạnh huyền DE nên: KI = KD = (1/2).ED (tính chất tam giác vuông)
Suy ra tam giác IKD cân tại K


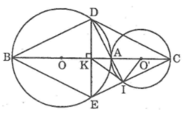
Vì đường tròn (O) và (O’) tiếp xúc ngoài tại A nên O, A và O’ thẳng hàng
Ta có: KB = KC (gt)
Trong đường tròn (O) ta có:
AB ⊥ DE tại K
Suy ra: KD = KE (đường kính vuông góc với dây cung)
Tứ giác BDCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có: BC ⊥ DE
Suy ra tứ giác BDCE là hình thoi.

Bài 1:
a: Ta có: ΔOBC cân tại O
mà OH là đường cao
nên OH là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}\)
=>\(\widehat{OCA}=90^0\)
=>AC là tiếp tuyến của (O)
b: Xét (O) có
ΔBKD nội tiếp
BD là đường kính
Do đó: ΔBKD vuông tại K
=>BK\(\perp\)KD tại K
=>BK\(\perp\)AD tại K
Xét ΔABD vuông tại B có BK là đường cao
nên \(AK\cdot AD=AB^2\left(1\right)\)
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AK\cdot AD=AH\cdot AO\)
Câu 8:
a: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>\(\widehat{CAB}+\widehat{CBA}=90^0\)
=>\(\widehat{CBA}=60^0\)
Xét ΔOBC có OB=OC và \(\widehat{OBC}=60^0\)
nên ΔOCB đều
=>BC=OB=R
=>BO=BM=R
=>B là trung điểm của OM
Xét ΔOCM có
CB là đường trung tuyến
CB=1/2OM
Do đó: ΔOCM vuông tại C
b: Ta có: OB+BM=OM
=>OM=R+R=2R
Ta có: ΔOCM vuông tại C
=>\(OC^2+CM^2=OM^2\)
=>\(CM^2=\left(2R\right)^2-R^2=3R^2\)

a: ΔOBC cân tại O
mà OA là đường cao
nên OA là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}=90^0\)
=>AC là tiếp tuyến của (O;R)
b: \(\widehat{MOA}+\widehat{COA}=\widehat{MOC}=90^0\)
\(\widehat{MAO}+\widehat{BOA}=90^0\)(ΔBAO vuông tại B)
mà \(\widehat{COA}=\widehat{BOA}\)
nên \(\widehat{MOA}=\widehat{MAO}\)
=>ΔMAO cân tại M