Cho AB//CD,Nối A với B, C với D và AB=CD(BC cùng phía so với AD).Chứng minh O là giao điểm của BD,AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
27 tháng 6 2016
a. Do AB//CD nên góc ABD = BDC, ADB = CBD. Suy ra \(\Delta ABD=\Delta CDB\left(g-c-g\right)\Rightarrow AB=CD,AD=BC\)
b. Dễ thấy \(\Delta AOB=\Delta COD\left(g-c-g\right)\Rightarrow OA=OC,OB=OD\)
c. Xét tam giác ABC có AM và BO là các đường trung tuyến nên E là trọng tâm, vậy OB = 2EO.
Tương tự DF=2FO. Mà OD = OB. Vậy BE = EF = DF.
24 tháng 12 2023
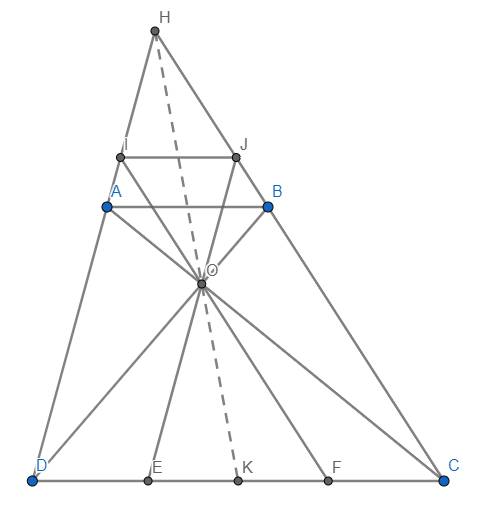
b) Theo Thales: \(\dfrac{DE}{DC}=\dfrac{AO}{AC};\dfrac{CF}{CD}=\dfrac{BO}{BD}\)
Theo câu a thì \(\dfrac{AO}{AC}=\dfrac{BO}{BD}\) \(\Rightarrow\dfrac{DE}{DC}=\dfrac{CF}{CD}\Rightarrow DE=CF\) (đpcm)
c) Từ \(DE=CF\Rightarrow\dfrac{DE}{EF}=\dfrac{CF}{EF}\)
Mà theo Thales: \(\dfrac{DE}{EF}=\dfrac{IO}{OF};\dfrac{CF}{EF}=\dfrac{JO}{OE}\)
Do đó \(\dfrac{IO}{OF}=\dfrac{JO}{OE}\) \(\Rightarrow\) IJ//CD//AB
d) Dùng định lý Menelaus đảo nhé bạn. Ta có \(\dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{OA}{OC}\) nê \(\dfrac{HA}{AD}.\dfrac{OC}{OA}=1\). Do K là trung điểm EF mà \(DE=CF\) nên K cũng là trung điểm CD hay \(\dfrac{KD}{KC}=1\). Do đó \(\dfrac{HA}{AD}.\dfrac{KD}{KC}.\dfrac{OC}{OA}=1\). Theo định lý Menalaus đảo \(\Rightarrow\)H, O, K thẳng hàng (đpcm)
3 tháng 12 2023
a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB\(\sim\)ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC}{OA}+1=\dfrac{OD}{OB}+1\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\)(2)
b: Xét ΔCAD có OE//AD
nên \(\dfrac{DE}{DC}=\dfrac{AO}{AC}\)(1)
Xét ΔBDC có OF//BC
nên \(\dfrac{CF}{CD}=\dfrac{BO}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{DE}{DC}=\dfrac{CF}{CD}\)
=>DE=CF
CT
25 tháng 4 2018
a) ABCD là hình thang nên AB//CD
CD=2AB ==>AB/CD=1/2
AB//CD, áp dụng định lý Ta-let, ta có
OA/OC=OB/OD=AB/CD=1/2
=>OA/OC=1/2 => OC=2OA
B) Ta có : OA/OC=OB/OD=AB/CD=1/2
==> OD/OB = 2 ==>OD = 2OB
*xét: OC/AC = 2OA/(OA + OC) = 2OA/(OA + 2OA) = 2OA/3OA = 2/3(1);
OD/BD = 2OB/(OD + OB) = 2OB/(2OB + OB) = 2/3(2)
*từ (1),(2) =>OC/AC = OD/BD = 2/3
=>O là trọng tâm tam giác FCD
c)
Vì một đường thẳng song song với AB và CD lần lượt cắt các đoạn thẳng AD, BD,AC và BC tại M, I,K và N nên KN//AB ,IM//AB và IN//AB
MI//AB, áp dụng hệ quả của định lý Ta-let, ta có
MI/AB = DM/AD = DI/IB (1)
IN//AB, áp dụng định lý Ta-let, ta có
CN/BC=DI/IB (2)
Từ (1) và (2), ta có
DM/AD=CN/BC
d)
KN//AB, áp dụng hệ quả của định lý Ta-let, ta có
KN/AB=CN/BC
Ta có :KN/AB=CN/BC và MI/AB=DM/AD
mà DM/AD=CN/BC nên KN/AB=MI/AB => KN=MI