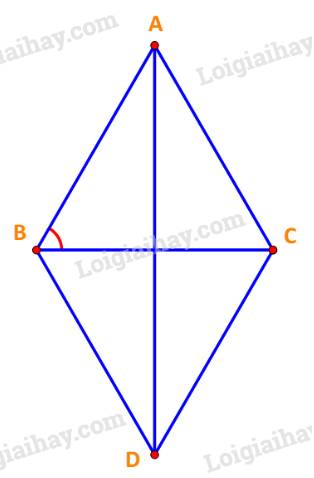
Cho tam giác ABC vuông tại A, biết AC=a và góc B= 60 độ.Tính độ dài các vec tơ :
a)\(\overrightarrow{AB}+\overrightarrow{AC}\) b)\(\overrightarrow{AB}-\overrightarrow{AC}\) c)\(\overrightarrow{AB}+\overrightarrow{BC}\) d)\(\overrightarrow{AB}-\overrightarrow{BC}\)