Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
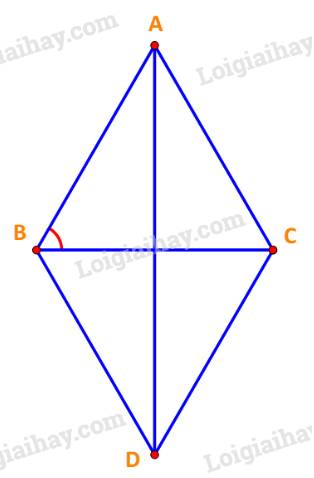
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = a.\)
Dựng hình bình hành ABDC tâm O như hình vẽ.
Ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Vì tứ giác ABDC là hình bình hành, lại có \(AB = AC = BD = CD = a\) nên ABDC là hình thoi.
\( \Rightarrow AD = 2AO = 2.AB.\sin B = 2a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 .\)
Vậy \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = a\) và \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \).


+) Ta có: \(AB \bot AC \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AC} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0\)
+) \(\overrightarrow {AC} .\overrightarrow {BC} = \left| {\overrightarrow {AC} } \right|.\left| {\overline {BC} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right)\)
Ta có: \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt 2 \Leftrightarrow \sqrt {2A{C^2}} = \sqrt 2 \)\( \Rightarrow AC = 1\)
\( \Rightarrow \overrightarrow {AC} .\overrightarrow {BC} = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1\)
+) \(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1\)

Dựng hình bình hành ABDC.
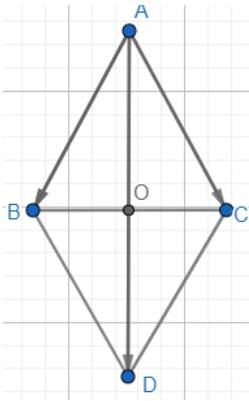
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)

Do tam giác ABC vuông tại A và \(\widehat{B}=30^o\) \(\Rightarrow C=60^o\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{BC}\right)=150^o;\)\(\left(\overrightarrow{BA},\overrightarrow{BC}\right)=30^o;\left(\overrightarrow{AC},\overrightarrow{CB}\right)=120^o\)
\(\left(\overrightarrow{AB},\overrightarrow{AC}\right)=90^o;\left(\overrightarrow{BC},\overrightarrow{BA}\right)=30^o\).Do vậy:
a) \(\cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)+\sin\left(\overrightarrow{BA},\overrightarrow{BC}\right)+\tan\frac{\left(\overrightarrow{AC},\overrightarrow{CB}\right)}{2}\)
\(=\cos150^o+\sin30^o+\tan60^o\)
\(=-\frac{\sqrt{3}}{2}+\frac{1}{2}+\sqrt{3}\)
\(=\frac{\sqrt{3}+1}{2}\)
b) \(\sin\left(\overrightarrow{AB},\overrightarrow{AC}\right)+\cos\left(\overrightarrow{BC},\overrightarrow{AB}\right)+\cos\left(\overrightarrow{CA},\overrightarrow{BA}\right)\)
\(=\sin90^o+\cos30^o+\cos0^o\)
\(=1+\frac{\sqrt{3}}{2}\)
\(=\frac{2+\sqrt{3}}{2}\)

a: \(\overrightarrow{BA}-\overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{CB}=\overrightarrow{CA}\)
b: lấy điểm H sao cho \(\overrightarrow{AH}=\overrightarrow{GC}\)
\(\overrightarrow{AH}=\overrightarrow{GC}\)
=>AH//GC và AH=GC
Xét tứ giác AHCG có
AH//CG
AH=GC
Do đó: AHCG là hình bình hành
ΔABC đều có G là trọng tâm
nên \(AG=GB=GC=\dfrac{a\sqrt{3}}{3}\)
\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AH}\right|\)
\(=\left|\overrightarrow{HA}+\overrightarrow{AB}\right|=\left|\overrightarrow{HB}\right|=HB\)
AHCG là hình bình hành
=>HC=AG và HC//AG
=>\(HC=\dfrac{a\sqrt{3}}{3}\)
ΔABC đều có G là trọng tâm
nên GB=GC=GA
GB=GC
AB=AC
Do đó: AG là đường trung trực của BC
=>AG\(\perp\)BC
mà CH//AG
nên CH\(\perp\)CB
=>ΔCHB vuông tại C
=>\(BH^2=HC^2+BC^2\)
=>\(BH^2=\left(\dfrac{a\sqrt{3}}{3}\right)^2+a^2=a^2+\dfrac{1}{3}a^2=\dfrac{4}{3}a^2\)
=>\(BH=a\cdot\dfrac{2\sqrt{3}}{3}\)
=>\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=BH=\dfrac{2a\sqrt{3}}{3}\)

Theo giả thiết ta có :
\(\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AB}+\overrightarrow{CA}\right)=0\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AB}-\overrightarrow{AC}\right)=0\)
\(\Leftrightarrow\overrightarrow{AB}^2-\overrightarrow{AC}^2=0\)
Ta suy ra ABC là tam giác có \(AB=AC\) (Tam giác cân tại A)

Do các vectơ đều nằm trên đường thẳng AB nên các vectơ này đều cùng phương với nhau.
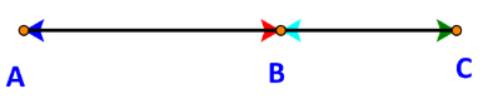
Dễ thấy:
Các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \) cùng hướng (từ trái sang phải.)
Các vectơ \(\overrightarrow {BA} ,\overrightarrow {CA} ,\overrightarrow {CB} \) cùng hướng (từ phải sang trái.)
Do đó, các cặp vectơ cùng hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \); \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \); \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CB} \);\(\overrightarrow {BA} \) và \(\overrightarrow {CB} \).
Các cặp vectơ ngược hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {AC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {BC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CB} \);
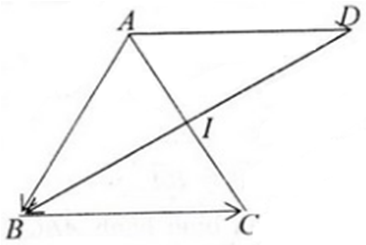
Tham khảo:
a) \(\)\(\overrightarrow {BA} + \overrightarrow {AC} = \overrightarrow {BC} \Rightarrow \left| {\overrightarrow {BC} } \right| = BC = a\)
b) Dựng hình bình hành ABDC, giao điểm của hai đường chéo là O ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
\(AD = 2AO = 2\sqrt {A{B^2} - B{O^2}} = 2\sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = a\sqrt 3 \)
\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt 3 \)
c) \(\overrightarrow {BA} - \overrightarrow {BC} = \overrightarrow {BA} + \overrightarrow {CB} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} \)
\( \Rightarrow \left| {\overrightarrow {BA} - \overrightarrow {BC} } \right| = \left| {\overrightarrow {CA} } \right| = CA = a\)