cho tam giác abc vuông tại a. gọi a,b,c lần lượt là chiều dài các cạnh bc, ca,ab. chứng minh Sabc=1/4(a+b+c)(b+c-a)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 10 2018
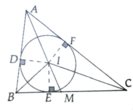
a, Áp dụng tính chất 2 tiếp tuyến tại A,B,C ta chứng minh được b + c - a 2 = AD
b, S A B C = S A I B + S B I C + S C I A
Mà ID = IE = IF = r => S A B C = p.r
c, Vì AM là phân giác của
B
A
C
^
=>
B
M
M
C
=
B
A
A
C
Áp dụng tính chất tỉ lệ thức thu được BM = a c c + b
12 tháng 12 2021
\(a,\) Vì M là trung điểm ND và BC nên BDCN là hình bình hành
\(b,\) Vì BDCN là hình bình hành nên \(BD\text{//}NC\) hay \(BD\text{//}NA\) và \(BD=NC=NA\) (N là trung điểm AC)
Do đó ABDN là hình bình hành
Mà \(\widehat{BAC}\equiv\widehat{NAB}=90^0\) nên ABDN là hình chữ nhật
\(c,\) Kẻ đường cao AH
\(\Rightarrow\left\{{}\begin{matrix}S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AH.2BM=AH.BM\\S_{ABM}=\dfrac{1}{2}AH.BM\end{matrix}\right.\\ \Rightarrow\dfrac{S_{ABM}}{S_{ABC}}=\dfrac{AH.BM}{2AH.BM}=\dfrac{1}{2}\\ \Rightarrow S_{ABC}=2S_{ABM}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2023
Đặt \(AF=x.AB\) ; \(AE=y.AC\) ; \(BD=z.BC\) (với \(0< x;y;z< 1\))
Do FH song song BK, áp dụng Talet: \(\dfrac{AF}{AB}=\dfrac{FH}{BK}\Rightarrow FH=\dfrac{AF}{AB}.BK=x.BK\)
Ta có: \(a=\dfrac{1}{2}FH.AE=\dfrac{1}{2}.x.BK.y.AC=xy.\left(\dfrac{1}{2}BK.AC\right)=xy.S\)
Tương tự: \(b=\left(1-x\right)z.S\) ; \(c=\left(1-y\right)\left(1-z\right)S\)
\(\Rightarrow abc=xyz\left(1-x\right)\left(1-y\right)\left(1-z\right).S^3\)
\(=x\left(1-x\right).y\left(1-y\right)z.\left(1-z\right).S^3\)
\(\le\dfrac{1}{4}\left(x+1-x\right).\dfrac{1}{4}\left(y+1-y\right).\dfrac{1}{4}\left(z+1-z\right)S^3=\dfrac{1}{64}S^3\)
Dấu "=" xảy ra khi \(x=y=z=\dfrac{1}{2}\) hay D, E, F lần lượt là trung điểm các cạnh tương ứng
2 tháng 1 2023
a: Xét ΔABC có
BE/BC=BD/BA
nên ED//AC và ED=AC/2
=>ED//AF và ED=AF
=>ADEF là hình bình hành
mà góc FAD=90 độ
nên ADEF là hình chữ nhật
b: Xét tứ giác BMAE có
D là trung điểm chung của BA vàME
EA=EB
Do đó: BMAE là hình thoi
c: \(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
S=1/2*3*4=6(cm2)
KT
29 tháng 3 2018
a) Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat{BAC}=\widehat{AHC}=90^0\)
\(\widehat{ABC}=\widehat{HAC}\) do cùng phụ với góc BAH )
suy ra: \(\Delta ABC~\Delta HAC\)
b) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)
Áp dụng hệ thức lượng ta có:
\(AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8\)cm
\(CH=\frac{AC^2}{BC}=\frac{8^2}{10}=6,4\)cm
\(BH=BC-HC=10-6,4=3,6\)cm
9 tháng 10 2021
b: Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
CM
14 tháng 6 2019
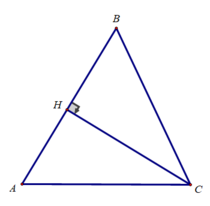
Kẻ đường cao CH của tam giác ABC. Ta có:
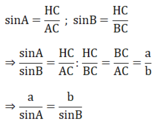
Chứng minh tương tự ta có:
