CMR cos15 độ:\(\frac{\sqrt{6}+\sqrt{2}}{4}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Đầu tiên bạn tự đi chứng minh hai công thức sau, do quá dài nên bạn có thể lên mạng tham khảo cách chứng minh:
\(\sin2a=2\sin a.\cos a\)
\(cos2a=cos^2a-sin^2a\)
Áp dụng hai công thức trên ta có:
\(sin30^o=2sin15^ocos15^o\Leftrightarrow sin15^ocos15^o=\frac{1}{4}\Leftrightarrow cos15^o=\frac{1}{4sin15^o}\)
\(cos30^o=cos^215^o-sin^215^o\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}=cos^215^o-sin^215^o\)
\(\Leftrightarrow\left(\frac{1}{4sin^215^o}\right)^2-sin^215^o=\frac{\sqrt{3}}{2}\)
\(\Leftrightarrow\frac{1}{16sin^415^o}-sin^215^o=\frac{\sqrt{3}}{2}\)
\(\Leftrightarrow-32sin^415^o-16sin^215^o\sqrt{3}+2=0\)
\(\Leftrightarrow sin^215^o=\frac{2-\sqrt{3}}{4}\left(sin^215^o\ge0\right)\)
\(\Leftrightarrow sin15^o=\sqrt{\frac{2-\sqrt{3}}{4}}=\sqrt{\frac{\left(\sqrt{3}-1\right)^2}{4\sqrt{2}}}=\frac{\sqrt{3}-1}{2\sqrt{2}}=\frac{\sqrt{6}-\sqrt{2}}{4}\left(đpcm\right)\)

Vẽ \(\Delta ABC\) vuông tại A có \(\widehat{C}=30^0\), đường phân giác CD.
CD là tia phân giác của \(\widehat{ACB}\)
\(\Rightarrow\widehat{ACD}=\widehat{BCD}=\dfrac{\widehat{ACD}}{2}=15^0\)
\(\Delta ABC\) vuông tại A có \(\widehat{C}=30^0\)
\(\Rightarrow\Delta ABC\) là nửa tam giác đều
\(\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{1}{2}BC\\AC=\dfrac{\sqrt{3}}{2}BC\end{matrix}\right.\)
\(\Delta ABC\) có CD là đường phân giác
\(\Rightarrow\tan15^0=\tan\widehat{ACD}=\dfrac{AD}{AC}=\dfrac{BD}{BC}=\dfrac{AD+BD}{AC+BC}=\dfrac{\dfrac{1}{2}BC}{\dfrac{\sqrt{3}}{2}BC+BC}=2-\sqrt{3}\) (áp dụng tính chất của dãy tỉ số bằng nhau_
\(1+\tan^215^0=\dfrac{1}{\cos^215^0}\)
\(\Rightarrow\cos15^0=\sqrt{\dfrac{1}{1+\tan^215^0}}=\sqrt{\dfrac{1}{1+\left(2-\sqrt{3}\right)^2}}\)
\(=\sqrt{\dfrac{1}{8-4\sqrt{3}}}=\sqrt{\dfrac{\left(8+4\sqrt{3}\right)}{64-48}}=\sqrt{\dfrac{\left(\sqrt{6}+\sqrt{2}\right)^2}{4^2}}=\dfrac{\sqrt{6}+\sqrt{2}}{4}\left(\text{đ}pcm\right)\)

\(0< 15^0< 90^0\Rightarrow sin,cos,tan\) đều dương
\(cos15=\sqrt{1-sin^215}=\sqrt{1-\left(\frac{\sqrt{6}-\sqrt{2}}{4}\right)^2}=\frac{\sqrt{6}+\sqrt{2}}{4}\)
\(tan15=\frac{sin15}{cos15}=2+\sqrt{3}\)
\(cot15=\frac{1}{tan15}=2-\sqrt{3}\)

a) AM ứng với cạnh huyền BC nên AM = \(\frac{1}{2}\) x BC = \(\frac{4}{2}\) = 2 cm
AH = tan\(\widehat{ACH}\)x HM = tan 150 x 2 = \(4-2\sqrt{3}\)cm
Sin \(\widehat{AMH}\)= \(\frac{AH}{AM}\)= \(\frac{4-2\sqrt{3}}{2}\) = \(2-\sqrt{3}\) cm
Định lí Pitago : AM2 = AH2 + HM2
HC = tan \(\widehat{ACH}\)x AH

Bài 1 :
a) \(Cos30^o=Cos\left(2.15^o\right)=2cos^215^o-1\)
\(\Rightarrow cos^215^o=\dfrac{cos30^o+1}{2}\)
\(\Rightarrow cos^215^o=\dfrac{\dfrac{\sqrt[]{3}}{2}+1}{2}\)
\(\Rightarrow cos^215^o=\dfrac{\sqrt[]{3}+2}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\sqrt[]{3}+2}}{2}\)
\(\Rightarrow cos15^o=\dfrac{2\sqrt[]{\sqrt[]{3}+2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{4\sqrt[]{3}+8}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6+2.2\sqrt[]{2}\sqrt[]{6}+2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\left(\sqrt[]{6}+\sqrt[]{2}\right)^2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6}+\sqrt[]{2}^{ }}{4}\left(dpcm\right)\)
a)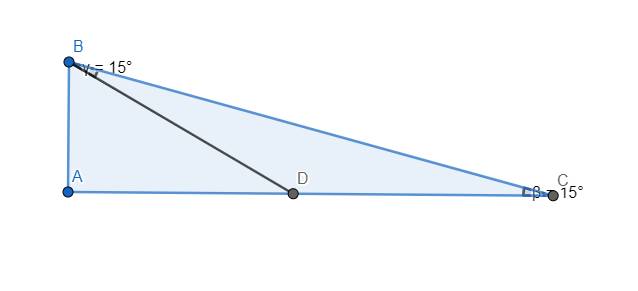
Dựng tam giác ABC vuông tại A với \(\widehat{C}=15^o\). Trên đoạn thẳng AC lấy điểm D sao cho \(\widehat{CBD}=15^o\). Không mất tính tổng quát, ta chuẩn hóa \(AB=1\). \(\Rightarrow\left\{{}\begin{matrix}BD=\dfrac{AB}{cos60^o}=2\\AD=AB.tan60^o=\sqrt{3}\end{matrix}\right.\)
Dễ thấy tam giác DBC cân tại D \(\Rightarrow BD=CD=2\) \(\Rightarrow AC=AD+DC=2+\sqrt{3}\)
\(\Rightarrow tanC=\dfrac{AB}{AC}=\dfrac{1}{2+\sqrt{3}}=2-\sqrt{3}\)
\(\Rightarrow\dfrac{sinC}{cosC}=2-\sqrt{3}\)
\(\Rightarrow sinC=\left(2-\sqrt{3}\right)cosC\)
Mà \(sin^2C+cos^2C=1\)
\(\Rightarrow\left(7-4\sqrt{3}\right)cos^2C+cos^2C=1\)
\(\Leftrightarrow\left(8-4\sqrt{3}\right)cos^2C=1\)
\(\Leftrightarrow cos^2C=\dfrac{1}{8-4\sqrt{3}}=\dfrac{2+\sqrt{3}}{4}\)
\(\Leftrightarrow cosC=\sqrt{\dfrac{2+\sqrt{3}}{4}}\) \(=\dfrac{\sqrt{2+\sqrt{3}}}{2}=\dfrac{\sqrt{8+4\sqrt{3}}}{4}\) \(=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)

Trước hết , ta cần chứng minh \(\frac{1}{\sqrt{n}+\sqrt{n+1}}=\sqrt{n+1}-\sqrt{n}\)(*) (Bạn tự chứng minh)
Đặt \(A=\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\frac{1}{\sqrt{5}+\sqrt{6}}+...+\frac{1}{\sqrt{79}+\sqrt{80}}\)
\(\Rightarrow2A=\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\frac{1}{\sqrt{5}+\sqrt{6}}+\frac{1}{\sqrt{5}+\sqrt{6}}+...+\frac{1}{\sqrt{79}+\sqrt{80}}+\frac{1}{\sqrt{79}+\sqrt{80}}\)
\(>\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\frac{1}{\sqrt{4}+\sqrt{5}}+...+\frac{1}{\sqrt{79}+\sqrt{80}}+\frac{1}{\sqrt{80}+\sqrt{81}}\)
Áp dụng (*) :\(\Rightarrow2A>\left(\sqrt{2}-\sqrt{1}\right)+\left(\sqrt{3}-\sqrt{2}\right)+\left(\sqrt{4}-\sqrt{3}\right)+\left(\sqrt{5}-\sqrt{4}\right)+...+\left(\sqrt{80}-\sqrt{79}\right)+\left(\sqrt{81}-\sqrt{80}\right)\)
\(\Rightarrow2A>\sqrt{81}-1=8\Rightarrow A>4\)(đpcm)