B=13+23+33+....+1003
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VK
3
18 tháng 10 2015
Ta có: B = (1 + 100) + (2 + 99) + ...+ (50 + 51) = 101. 50
Để chứng minh A chia hết cho B ta chứng minh A chia hết cho 50 và 101
Ta có: A = (13 + 1003) + (23 + 993) + ... +(503 + 513)
= (1 + 100)(12 + 100 + 1002) + (2 + 99)(22 + 2. 99 + 992) + ... + (50 + 51)(502 + 50. 51 + 512) =
101(12 + 100 + 1002 + 22 + 2. 99 + 992 + ... + 502 + 50. 51 + 512) chia hết cho 101 (1)
Lại có: A = (13 + 993) + (23 + 983) + ... + (503 + 1003)
Mỗi số hạng trong ngoặc đều chia hết cho 50 nên A chia hết cho 50 (2)
Từ (1) và (2) suy ra A chia hết cho 101 và 50 nên A chi hết cho B
18 tháng 10 2015
Ta có: B = (1 + 100) + (2 + 99) + ...+ (50 + 51) = 101. 50
Để chứng minh A chia hết cho B ta chứng minh A chia hết cho 50 và 101
Ta có: A = (13 + 1003) + (23 + 993) + ... +(503 + 513)
= (1 + 100)(12 + 100 + 1002) + (2 + 99)(22 + 2. 99 + 992) + ... + (50 + 51)(502 + 50. 51 + 512) =
101(12 + 100 + 1002 + 22 + 2. 99 + 992 + ... + 502 + 50. 51 + 512) chia hết cho 101 (1)
Lại có: A = (13 + 993) + (23 + 983) + ... + (503 + 1003)
Mỗi số hạng trong ngoặc đều chia hết cho 50 nên A chia hết cho 50 (2)
Từ (1) và (2) suy ra A chia hết cho 101 và 50 nên A chi hết cho B
TN
0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
Bài 1:
13 + 23 = 1 + 8 = 9 = 32 (là một số chính phương)
13 + 23 + 33 = 1 + 8 + 27 = 36 = 62 (là một số chính phương)
13 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100 = 102 (là số cp)
13 + 23 + 33 + 43 + 53 = 1 + 8 + 27 + 64 + 125 = 225 = (15)2 là số cp
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
Bài 2:
1262 + 1 = \(\overline{..6}\) + 1 = \(\overline{...7}\) (không phải số chính phương)
100! + 8 = \(\overline{...0}\) + 8 = \(\overline{...8}\) (không phải là số chính phương)
1012 - 3 \(\overline{..01}\) - 3 = \(\overline{...8}\) (không phải là số chính phương)
107 + 7 = \(\overline{..0}\) + 7 = \(\overline{..7}\) (không phải là số chính phương)
11 + 112 + 113 = \(\overline{..1}\)+ \(\overline{..1}\)+ \(\overline{..1}\) = \(\overline{...3}\) (không phải số chính phương)
VT
1
13 tháng 9 2021
\(A=\frac{7}{3\times13}+\frac{7}{13\times23}+...+\frac{7}{53\times63}\)
\(A=\frac{7}{10}.\left[\left(\frac{1}{3}-\frac{1}{13}\right)+\left(\frac{1}{13}-\frac{1}{23}\right)+....+\left(\frac{1}{53}-\frac{1}{63}\right)\right]\)
\(A=\frac{7}{10}.\left(\frac{1}{3}-\frac{1}{13}+\frac{1}{13}-\frac{1}{23}+....+\frac{1}{53}-\frac{1}{63}\right)\)
\(A=\frac{7}{10}.\left(\frac{1}{3}-\frac{1}{63}\right)\)
\(A=\frac{7}{10}.\frac{20}{63}\)
\(A=\frac{2}{9}\)
NN
0
DN
1
PT
19 tháng 4 2018
A=7*(1/3*13+1/13*23+1/23*33+1/33*43+1/43*53+1/53*63)
A=7/10(1/3-1/13+1/13-1/23+1/23-1/33+1/33-1/43+1/43-1/53+1/53-1/63)
A=7/10*(1/3-1/63)
A=7/10*20/63
A=2/9
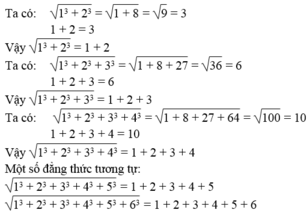
B = (1 + 2 + 3 + ....... + 100)2
B = (100.101 : 2 )2
B = 5050 2 = 25502500