Cho tam giác ABC vuông tại A có AB > AC. tia phân giác của góc B cắt AC ở D, đường thảng qua D và vuông góc với BC tại H . Trên tia AC lấy điểm E sao cho AE = AB, đường thẳng qua E vuông gosdc với AE cắt tia DH ở K.
CMR BD là trung trực của đoạn thẳng AH

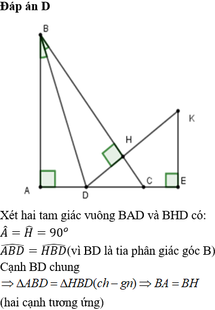
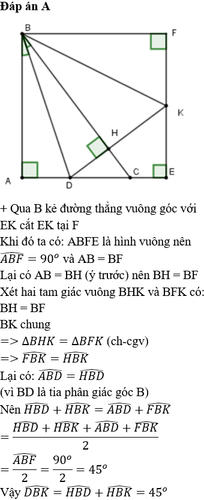
Xét \(\Delta BAD\)(\(\widehat{A}=90^o\))và \(\Delta BHD\)(\(\widehat{H}=90^o\))có:
\(\widehat{ABD=\widehat{HBD}}\)(gt)
BD: cạnh chung
=> \(\Delta ABD=\Delta HBD\left(CH-GN\right)\)
=> AB=BH; AD=DC (2 cạnh t/ứng)
và \(\widehat{BDA=\widehat{BDC}}\)(2 góc t/ứng)
Xét \(\Delta ABH\)cân tại B(vì AB=BH[cmt]) có : BD là đường p.g
=> B là điểm thuộc đường trung trực AH (1)
Xét \(\Delta ADH\)cân tại D(vì AD=DH(cmt)) có: DB là đường p.g ( vì \(\widehat{BDA=\widehat{BDC}}\))
=> D là điểm thuộc đường trung trực AH (2)
Từ (1) và (2)=> BD là trung trực của đt AH
+ Xét \(\Delta ABD\)vuông tại A và \(\Delta HBD\)vuông tại H ( vì \(DH\perp BC\))
Có : BD là cạnh chung
\(\widehat{ABD}=\widehat{HBD}\)( Vì BD là p/g của góc B) => \(\Delta ABD=\Delta HBD\)( canh huyền-góc nhọn)
=> AB = HB
+ Gọi I là giao điểm của BD và AH
CM đc : \(\Delta ABI=\Delta HBI\)(c-g-c)
=> IA = IH ( 2 cạnh tương ứng) (1)
và \(\widehat{BIA}=\widehat{BIH}\)( 2 góc t.ư)
Vì \(\widehat{BIA}=\widehat{BIH};\widehat{BIA}+\widehat{BIH}=180^o\)( 2 góc k.bù)
=> \(\widehat{BIA}=\widehat{BIH}=\frac{180^o}{2}=90^o\Rightarrow BD\perp AH\)tại I (2)
Từ (1),(2) => BD là trung trực của đth AH