Tìm x,y thỏa mãn : 32x+1.7y=9.21x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^3-32x=-y\left(2x+1\right)\Rightarrow-y=\dfrac{x^3-32x}{2x+1}\)
\(\Leftrightarrow-8y=\dfrac{8x^3-256x}{2x+1}=4x^2-2x-127+\dfrac{127}{2x+1}\)
\(\Rightarrow2x+1=Ư\left(127\right)=\left\{-127;-1;1;127\right\}\)
\(\Rightarrow\left[{}\begin{matrix}2x+1=-127\left(loại\right)\\2x+1=-1\left(loại\right)\\2x+1=1\left(loại\right)\\2x+1=127\end{matrix}\right.\) \(\Rightarrow x=63\Rightarrow y=-1953< 0\) (loại)
Pt đã cho không có nghiệm nguyên dương

Cách khác: Ta có \(x^2y+2xy+y=32x\)
\(\Leftrightarrow y\left(x+1\right)^2=32x\).
Từ đó \(32x⋮\left(x+1\right)^2\).
Mà \(\left(x,\left(x+1\right)^2\right)=1\) nên \(32⋮\left(x+1\right)^2\Leftrightarrow\left(x+1\right)^2\in\left\{1;4;16\right\}\).
+) Với \(\left(x+1\right)^2=1\Rightarrow x=0\) (loại)
+) Với \(\left(x+1\right)^2=4\Rightarrow x=1;y=8\)
+) Với \(\left(x+1\right)^2=16\Rightarrow x=3;y=6\).
Vậy...
\(\Leftrightarrow y\left(x^2+2x+1\right)-32x-32=-32\)
\(\Leftrightarrow y\left(x+1\right)^2-32\left(x+1\right)=-32\)
\(\Leftrightarrow\left(x+1\right)\left(xy+y-32\right)=-32\)
Do \(x+1\ge2\) nên chỉ có các trường hợp sau:
TH1: \(\left\{{}\begin{matrix}x+1=2\\xy+y-32=-16\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}x+1=4\\xy+y-32=-8\end{matrix}\right.\)
TH3: \(\left\{{}\begin{matrix}x+1=8\\xy+y-32=-4\end{matrix}\right.\)
TH4: \(\left\{{}\begin{matrix}x+1=16\\xy+y-32=-2\end{matrix}\right.\)
TH5: \(\left\{{}\begin{matrix}x+1=32\\xy+y-32=-1\end{matrix}\right.\)
Bạn tự giải

\(x^2y+2xy+y=32x\)
\(\Leftrightarrow y\left(x^2+2x+1\right)=32\left(x+1\right)-32\)
\(\Leftrightarrow y\left(x+1\right)^2=32\left(x+1\right)-32\)
\(\Leftrightarrow\)\(\left(x+1\right)\left(32-xy-y\right)=32\)
Vì x, y nguyên dương nên:
...( tự làm nhé!)

Ta có
x + 2 y = m + 3 2 x − 3 y = m ⇔ 2 x + 4 y = 2 m + 6 2 x − 3 y = m ⇔ x + 2 y = m + 3 7 y = m + 6 ⇔ x = 5 m + 9 7 y = m + 6 7
Hệ phương trình có nghiệm duy nhất ( x ; y ) = 5 m + 9 7 ; m + 6 7
Lại có x + y = −3 hay 5 m + 9 7 + m + 6 7 = − 3 ⇔ 5m + 9 + m + 6 = −21
⇔ 6m = −36 ⇔ m = −6
Vậy với m = −6 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x + y = −3
Đáp án: A

Đáp án A

Vậy với m = -6 thì hệ phương trình có nghiệm duy nhất (x, y) thỏa mãn x + y = -3


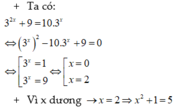

\(=>3^{2x+1}.7^y=3^2.3^x.7^x=3^{x+2}.7^x=>3^{2x+1}:3^{x+2}=7^x:7^y\)
\(=>3^{x-1}=7^{x-y}\)
Mà \(\left(3,7\right)=1\) nen \(x-1=x-y=0=>x=y=1\)
Vậy x=y=1