Trong mặt phẳng cho 10 điểm A,Az;A:AriAs;AA);AA);A, đôi một không trung nhau. Hỏi thành lập được bao véc tơ có các điểm đầu và điểm cuối là các điểm đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 7 2018
Đáp án B
Muốn khoảng cách giữa hai mặt phẳng (P) và (Q) lớn hơn 0 thì trước hết hai mặt phẳng đó phải song song (nếu hai mặt phẳng đó trùng nhau hoặc cắt nhau thì khoảng cách giữa chúng sẽ bằng 0). Do đó ta có:
26 tháng 10 2021
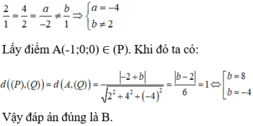
a, Vì \(\widehat{xOy}+\widehat{OAz}=140^0+40^0=180^0\) mà 2 góc này ở vị trí TCP nên Az//Oy
b, Gọi Om,On lần lượt là p/g \(\widehat{xOy};\widehat{OAt}\)
Ta có \(\widehat{OAt}=180^0-\widehat{OAz}=140^0\left(kề.bù\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{mOx}=\dfrac{1}{2}\widehat{xOy}=70^0\\\widehat{nAO}=\dfrac{1}{2}\widehat{OAt}=70^0\end{matrix}\right.\Rightarrow\widehat{mOx}=\widehat{nAO}\) mà 2 góc này ở vị trí SLT nên Om//On
Do đó 2 đg p/g của \(\widehat{xOy}\) và \(\widehat{OAt}\) song song vs nhau
26 tháng 10 2021
a, Vì \(\widehat{OAz}+\widehat{xOy}=140^0+40^0=180^0\) mà 2 góc này ở vị trí tcp nên Az//Oy
b, Vì At đối Az nên \(\widehat{OAt}=180^0-\widehat{OAz}=140^0\left(kề.bù\right)\)
Gọi Om là p/g \(\widehat{xOy}\), On là p/g \(\widehat{OAt}\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{mOx}=\dfrac{1}{2}\widehat{xOy}=70^0\\\widehat{OAn}=\dfrac{1}{2}\widehat{OAt}=70^0\end{matrix}\right.\\ \Rightarrow\widehat{mOx}=\widehat{OAn}\)
Do đó ta đc dpcm
CM
30 tháng 6 2018
Chọn C
Ta có:
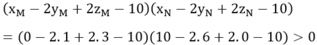
Nên hai điểm M và N nằm cùng phía so với mặt phẳng (P)
Ta luôn có: 
, nên |IM - IN| lớn nhất khi và chỉ khi I là giao điểm của đường thẳng MN với mặt phẳng (P).
Đường thẳng MN có vec-tơ chỉ phương 
, nên phương trình đường thẳng MN là: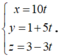 
Tọa độ giao điểm I của đường thẳng MN với mặt phẳng (P) ứng với t là nghiệm phương trình:
10t - 2(1+5t) + 2(3-3t) - 10 = 0 <=> t = -1
Do đó I (-10; -4; 6), từ đó ta có a = -4 và b = 6, nên T = -4 + 6 = 2.
CM
4 tháng 2 2019
Đáp án D
Ta có n ( Q ) → = 1 ; − 2 ; − 2
Vì (P) song song với (Q) nên (P) nhận n ( Q ) → = 1 ; − 2 ; − 2 làm vectơ pháp tuyến.
Mặt phẳng (P) đi qua A(-1;3;-2) và nhận n ( Q ) → = 1 ; − 2 ; − 2 làm vectơ pháp tuyến có phương trình là:
1 x + 1 − 2 y − 3 − 2 z + 2 = 0 ⇔ x − 2 y − 2 z + 3 = 0