giải phương trình:
\(\sqrt{1-2x^2}=x-1\)
mình giải ra hình như là vô nghiệm vì điều kiện phương trình sai sai
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 12 2018
Đáp án: A
Bước 1 sai vì giả sử phản chứng sai, phải giả sử phương trình vô nghiệm và a, c trái dấu.
. Ta có:
CM
9 tháng 3 2017
a) Sai lầm là coi -2 là hạng từ và chuyển vế hạng tử này trong khi -2 là một nhân tử.
Lời giải đúng:
-2x > 23
⇔ x < 23 : (-2) (chia cho số âm nên đổi chiều)
⇔ x < -11,5
Vậy nghiệm của bất phương trình là x < -11,5
b) Sai lầm là nhân hai vế của bất phương trình với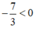 
mà không đổi chiều bất phương trình.
Lời giải đúng:
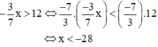
Vậy nghiệm của bất phương trình là x < -28
LA
29 tháng 3 2022
a) 2x2 - 6x -1 = 0
delta phẩy = 9 + 2 = 11 = (\(\sqrt{11}\))2
x1 = \(\dfrac{3+\sqrt{11}}{2}\)
x2 = \(\dfrac{3-\sqrt{11}}{2}\)
b) xét delta phẩy có :
9 - 2.(2m-5) = 19 - 4m
+) điều kiện để phương trình vô nghiệm là 19 - 4m < 0 => m > \(\dfrac{19}{4}\)
+) điều kiện để phương trình có nghiệm kép là 19 - 4m = 0 => m = \(\dfrac{19}{4}\)
+) điều kiện để phương trình có 2 nghiệm phân biệt là 19 - 4m > 0
=> m < \(\dfrac{19}{4}\)
MT
15 tháng 1 2016
a)Để PT ( 3m - 1)x + 3 = 0 là PT bậc nhất thì:
3m-1 khác 0
=>m khác 1/3
b) PT có nghiệm x=-3 thì:
(3m-1).(-3)+3=0
<=>-9m+3+3=0
<=>-9m=-6
<=>m=2/3
Vậy m=2/3
c)Để PT vô nghiệm thì: 3m-1=0
=>m=1/3
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
Thay \(x = 2\) vào phương trình \(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \) ta thấy không thỏa mãn vì dưới dấu căn là \( - 1\) không thỏa mãn
Vậy \(x = 2\) không là nghiệm của phương trình do đó lời giải như trên là sai.
AH
Akai Haruma
Giáo viên
3 tháng 8 2021
Lời giải:
PT $\Leftrightarrow (x+1)^2+|x+1|-(m+1)=0$
$\Leftrightarrow |x+1|^2+|x+1|-(m+1)=0$
Đặt $|x+1|=t(t\geq 0)$ thì: $t^2+t-(m+1)=0(*)$
Với $m=1$ thì $t^2+t-2=0$
$\Leftrightarrow (t-1)(t+2)=0$
Vì $t\geq 0$ nên $t=1\Leftrightarrow |x+1|=1$
$\Leftrightarrow x+1=\pm 1\Leftrightarrow x=0$ hoặc $x=-2$
Để pt vô nghiệm thì $(*)$ chỉ có nghiệm âm hoặc vô nghiệm.
PT $(*)$ chỉ có nghiệm âm khi \(\left\{\begin{matrix} \Delta (*)=1+4(m+1)\geq 0\\ S=-1< 0\\ P=-(m+1)<0\end{matrix}\right.\Leftrightarrow m>-1\)
Để $(*)$ vô nghiệm khi $\Delta=4m+5< 0$
$\Leftrightarrow m< \frac{-5}{4}$
Vậy $m>-1$ hoặc $m< \frac{-5}{4}$
19 tháng 11 2023
ĐKXĐ: \(\left\{{}\begin{matrix}2x+5>=0\\4-2x>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x>=-5\\2x< =4\end{matrix}\right.\Leftrightarrow-\dfrac{5}{2}< =x< =2\)
\(x^2+\sqrt{2x+5}+\sqrt{4-2x}=4x-1\)
=>\(x^2-4+\sqrt{2x+5}-3+\sqrt{4-2x}=4x-1-7\)
=>\(\left(x-2\right)\left(x+2\right)+\dfrac{2x+5-9}{\sqrt{2x+5}+3}+\sqrt{4-2x}=4x-8\)
=>\(\left(x-2\right)\left[\left(x+2\right)+\dfrac{2}{\sqrt{2x+5}+3}-4\right]+\sqrt{4-2x}=0\)
=>\(-\left(2-x\right)\left[\left(x-2\right)+\dfrac{2}{\sqrt{2x+5}+3}\right]+\sqrt{2\left(2-x\right)}=0\)
=>\(\sqrt{2-x}\left[-\sqrt{2-x}\left(x-2+\dfrac{2}{\sqrt{2x+5}+3}\right)+\sqrt{2}\right]=0\)
=>\(\sqrt{2-x}=0\)
=>x=2(nhận)