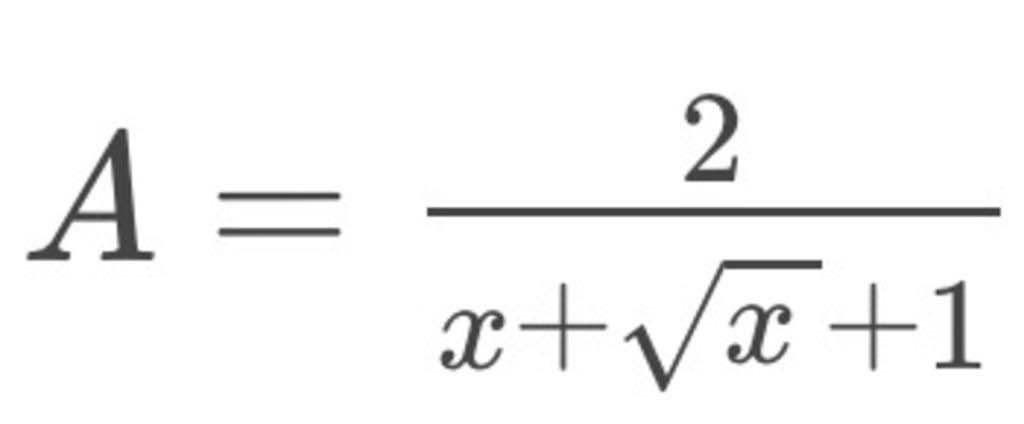ĐK: x≥0, x khác 1
Chứng minh rằng 0<A<2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
Chắc là a;b;c hết chứ?
\(VT=\dfrac{a}{a+b+c+b-a}+\dfrac{b}{a+b+c+c-b}+\dfrac{c}{a+b+c+a-c}\)
\(VT=\dfrac{a}{c+2b}+\dfrac{b}{a+2c}+\dfrac{c}{b+2a}=\dfrac{a^2}{ac+2ab}+\dfrac{b^2}{ab+2bc}+\dfrac{c^2}{bc+2ac}\)
\(VT\ge\dfrac{\left(a+b+c\right)^2}{3\left(ab+bc+ca\right)}\ge\dfrac{3\left(ab+bc+ca\right)}{3\left(ab+bc+ca\right)}=1\) (đpcm)
11 tháng 9 2021
cho x,y,z>0 ,x+y+z=1 chu nhi?
\(\Rightarrow\dfrac{x}{x+y+z+y-x}=\dfrac{x}{2y+z}\)
\(\Rightarrow\dfrac{y}{1+z-y}=\dfrac{y}{x+y+z+z-y}=\dfrac{y}{2z+x}\)
\(\Rightarrow\dfrac{z}{1+x-z}=\dfrac{z}{x+y+z+x-z}=\dfrac{z}{2x+y}\)
\(\Rightarrow A=\dfrac{x}{2y+z}+\dfrac{y}{2z+x}+\dfrac{z}{2x+y}=\dfrac{x^2}{2xy+xz}+\dfrac{y^2}{2zy+xy}+\dfrac{z^2}{2xz+xz}\ge\dfrac{\left(x+y+z\right)^2}{3\left(xy+yz+xz\right)}=1\)
dau"=" xay ra<=>x=y=z=1/3
TH
1
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 10 2021
\(\left(a-1\right)\left(b-1\right)\left(c-1\right)=\left(a-1\right)\left(bc-b-c+1\right)\)
\(=abc-\left(ab+bc+ca\right)+a+b+c-1\)
\(=abc-abc+1-1=0\) (đpcm)
NC
0
QQ
0
16 tháng 6 2015
P(x) = ax+ b = 0 =
=> ãx = -b => x = -b / a = x0
1/ x0 = 1/-b/a = a/-b thay vao Q(x) ta co
Q(x) = b. -a /b + a = -a + a = 0
Vậy x0 là nghiệm của P(x)=ax+b (a khác 0, b khác 0) thì 1/x0 là nghiệm của đa thức Q(x)=bx+a
22 tháng 8 2021
Ta có: \(P=A\cdot B\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)