Cho hình thang ABCD. Gọi E là trung điểm của cạnh bên AD, F là trung điểm của cạnh bên BC.Chứng mình:EF//AB
(Giải theo cách lớp 7 được ko? nếu được thì giải giùm?)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

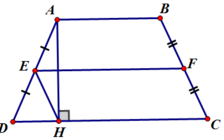
*Có AH ⊥ CD ⇒ ∆ AHD vuông tại H
E là trung điểm của AD ⇒ HE là trung tuyến ứng với cạnh huyền AD
⇒ HE = 1/2 AD (1)
*F là trung điểm của BC ⇒ CF = 1/2 BC (2)
Mà ABCD là hình thang cân ⇒ BC = AD (3)
Từ (1), (2) và (3) ta có: HE = CF (*)
*Mặt khác: EH = ED = 1/2 AD (Chứng minh trên)
⇒ ∆ EHD cân tại E
⇒ ∠ (EHD) = ∠ (EDH)
Mà ∠ (EDH) = ∠ (FCH) (góc đáy hình thang cân)
⇒ ∠ (FCH) = ∠ (EHD) (cùng bằng ∠ (EDH))
⇒EH // FC (2 góc ở vị trí đồng vị bằng nhau) (**)
Từ (*) và (**) ⇒ EFCH là hình bình hành (1 cặp cạnh song song và bằng nhau)

Lời giải:
$\frac{S_{DFI}}{S_{DIC}}=\frac{FI}{IC}$
$\frac{S_{FEI}}{S_{IEC}}=\frac{FI}{IC}$
Đặt $\frac{FI}{IC}=a$ thì:
$S_{DFI}=a\times S_{DIC}$
$S_{FEI}=a\times S_{IEC}$
$S_{DFI}+S_{FEI}=a\times (S_{DIC}+S_{IEC})$
$S_{DEF}=a\times S_{DEC}$
$\frac{AE\times DF}{2}=a\times \frac{DC\times AD}{2}$
$\frac{2\times 2}{2}=a\times \frac{4\times 4}{2}$
$2=a\times 8$
$a=\frac{1}{4}$
Vì $S_{DIC}+S_{DFI}=S_{DFC}=\frac{DF\times DC}{2}=\frac{2\times 4}{2}=4$
Mà tỷ số $\frac{S_{DFI}}{S_{DIC}}=\frac{FI}{IC}=\frac{1}{4}$
Theo bài toán tổng và tỷ suy ra $S_{DIC}=4:(1+4)\times 4=3,2$ (cm vuông)
$S_{IEC}=S_{DEC}-S_{DIC}=8-3,2=4,8$ (cm vuông)
$S_{IEBC}=S_{IEC}+S_{EBC}=4,8+\frac{EB\times BC}{2}=4,8+\frac{2\times 4}{2}=8,8$ (cm vuông)

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Trần Nhật Duy - Toán lớp 8 - Học toán với OnlineMath

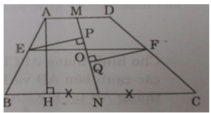
Ta có MA = MD, NC = NB (gt) và AD // BC.
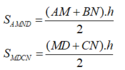
⇒ SAMND = SMCDN (các hình thang có các đáy bằng nhau và chung đường cao)
Do EF // AD nên đường cao từ E và F xuống AD bằng nhau, lại có AM = DM
⇒ SAEM = SDFM
Tương tự SBEN = SNFC
⇒ SAMNB - (SAEM + SBEN) = SDMNC - (SBEN + SNFC)
hay SEMN = SFMN
Hai tam giác trên có chung cạnh MN nên đường cao tương ứng bằng nhau hay EP = FQ
Xét ΔEPO và ΔFQO có:
∠EOP = ∠QOF (đối đỉnh)
EP = PQ (cmt)
∠EPO = ∠FQO = 90o
Do đó ΔEPO = ΔFQO (ch–gn) ⇒ OE = OF hay O là trung điểm của EF.