Một vật chuyển động với phương trình s(t)4t2+t3, trong đó t>0, t tính bằng s, s(t) bằng m. Tìm gia tốc của vật tại thời điểm vận tốc của vật bằng 11
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 8 2017
Chọn D.
Phương pháp : Sử dụng ý nghĩa cơ học của đạo hàm cấp hai.
TK
17 tháng 9 2021
Phương trình chuyển động của vật là:
\(x=4t^2+20t\left(cm,s\right)\)
\(\Rightarrow a=8\left(\dfrac{cm}{s^2}\right);v_0=20\left(\dfrac{cm}{s}\right)\)
a, Vận tốc của vật ở thời điểm t=3s
\(v=20+8\cdot3=44\left(\dfrac{cm}{s}\right)\)
b, Quãng đường đi dc ở từ thời điểm 2s đến t=5s
\(s=4\cdot\left(5-2\right)^2+20\cdot\left(5-2\right)=96\left(cm\right)\)
Tốc độ trung bình trong khoảng thời gian này là
\(v_{tb}=\dfrac{96}{5-2}=32\left(\dfrac{cm}{s}\right)\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
\(v\left(t\right)=s'\left(t\right)=0,8\pi cos\left(0,8\pi t+\dfrac{\pi}{3}\right)\\ a\left(t\right)=v'\left(t\right)=-0,64\pi^2sin\left(0,8\pi t+\dfrac{\pi}{3}\right)\)
Vì:
\(v\left(t\right)=0\\ \Leftrightarrow0,8\pi cos\left(0,8\pi t+\dfrac{\pi}{3}\right)=0\\ \Leftrightarrow0,8\pi t+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi,k\in Z\\ \Leftrightarrow0,8\pi t=\dfrac{\pi}{6}+k\pi\\ \Leftrightarrow t=\dfrac{5}{24}+\dfrac{5k}{4}\)
Thời điểm vận tốc bằng 0, giá trị tuyệt đối của vật là
\(\left|a\left(\dfrac{5}{25}+\dfrac{5k}{4}\right)\right|=\left|-0,64\pi^2sin\left[0,8\pi\left(\dfrac{5}{24}+\dfrac{5k}{4}\right)+\dfrac{\pi}{3}\right]\right|\\ =0,64\pi^2\left|sin\left(\dfrac{\pi}{2}+k\pi\right)\right|\\ =0,64\pi^2\approx6,32\)
\(\Rightarrow\) Chọn C.
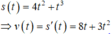
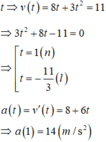
\(v\left(t\right)=s'\left(t\right)=3t^2+8t\)
\(a\left(t\right)=v'\left(t\right)=6t+8\)
Tại thời điểm vận tốc của vật bằng 11
\(\Leftrightarrow3t^2+8t=11\Leftrightarrow3t^2+8t-11=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-\frac{11}{3}< 0\left(l\right)\end{matrix}\right.\)
\(\Rightarrow a=6.1+8=14\left(m/s^2\right)\)