Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(-1\le sin\left(1,5t+\dfrac{\pi}{3}\right)\le1\Leftrightarrow-3\le-3sin\left(1,5t+\dfrac{\pi}{3}\right)\le3\Leftrightarrow-3\le v\le3\)
a, Vận tốc con lắc đạt giá trị lớn nhất khi
\(-3sin\left(1,5t+\dfrac{\pi}{3}\right)=3\\ \Leftrightarrow sin\left(1,5t+\dfrac{\pi}{3}\right)=-1\\ \Leftrightarrow sin\left(1,5t+\dfrac{\pi}{3}\right)=sin\left(-\dfrac{\pi}{2}\right)\\ \Leftrightarrow\left[{}\begin{matrix}1,5t+\dfrac{\pi}{3}=-\dfrac{\pi}{2}+k2\pi\\1,5t+\dfrac{\pi}{3}=\pi+\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\Leftrightarrow t=-\dfrac{5\pi}{9}+\dfrac{k4\pi}{3},k\in Z\)
Vậy vận tốc con lắc đạt giá trị lớn nhất tại các thời điểm \(t=-\dfrac{5\pi}{9}+\dfrac{k4\pi}{3},k\in Z\)
b, Để vận tốc con lắc bằng 1,5cm/s thì
\(-3sin\left(1,5t+\dfrac{\pi}{3}\right)=1,5\\ \Leftrightarrow sin\left(1,5t+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\\ \)
\(\Leftrightarrow\left[{}\begin{matrix}1,5t+\dfrac{\pi}{3}=-\dfrac{\pi}{6}+k2\pi\\1,5t+\dfrac{\pi}{3}=\pi+\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\\ \)
\(\Leftrightarrow \left[{}\begin{matrix}t=-\dfrac{\pi}{3}+\dfrac{k4\pi}{3}\\t=\dfrac{5\pi}{9}+\dfrac{k4\pi}{3}\end{matrix}\right.\) \(\left(k\in Z\right)\)

Vận tốc tại thời điểm t là \(v\left( t \right) = s'\left( t \right) = 0,5.2\pi \cos \left( {2\pi t + \frac{\pi }{5}} \right) = \pi \cos \left( {2\pi t + \frac{\pi }{5}} \right)\)
Gia tốc tức thời của vật tại thời điểm t là \(a\left( t \right) = v'\left( t \right) = - \pi .2\pi \sin \left( {2\pi t + \frac{\pi }{5}} \right) = - 2{\pi ^2}\sin \left( {2\pi t + \frac{\pi }{5}} \right)\)
Tại thời điểm t = 5 giây, gia tốc của vật là \(a\left( 5 \right) = - 2{\pi ^2}\sin \left( {2\pi .5 + \frac{\pi }{5}} \right) \approx - 11,6\)(cm/s2)

a, Quãng đường vật đã rơi tại thời điểm t = 2s sau khi thả vật đó là:
\(s\left(2\right)=0,81\cdot2^2=3,24\left(m\right)\)
b, Ta có: \(s'\left(t\right)=1,62t\Rightarrow s''\left(t\right)=1,62\)
Gia tốc của vật đã rơi tại thời điểm t = 2s sau khi thả vật đó là:
\(a\left(2\right)=s''\left(2\right)=1,62\left(m/s^2\right)\)

\(v\left(t\right)=s'\left(t\right)=4\left[cos\left(2\pi t-\dfrac{\pi}{8}\right)\right]'\\ =-4\left(2\pi t-\dfrac{\pi}{8}\right)'sin\left(2\pi t-\dfrac{\pi}{8}\right)\\ =-8\pi sin\left(2\pi t-\dfrac{\pi}{8}\right)\)
Vận tốc của vật khi t = 5s là \(v\left(5\right)=-8\pi sin\left(10\pi-\dfrac{\pi}{8}\right)\approx9,6\left(m/s\right)\)

1 vòng tròn tương ứng với 2π hay \({360^o}\). Vậy \(3\frac{1}{5}\) vòng là \(3\frac{1}{5}{.360^o} = 1{\rm{ }}152^\circ \).
Đáp án: C
\(3\dfrac{1}{5}=\dfrac{16}{5}\) vòng ngược chiều kim đồng hồ :
\(\dfrac{16}{5}.2\pi=\dfrac{32\pi}{5}=1152^o\rightarrow Chọn\) \(C\)

a) Khi a = 1dm:
Diện tích một mặt `(S) = a^2 = 1^2 = 1dm^2`
Thể tích `(V) = a^3 = 1^3 = 1dm^3`
Khi a = 3dm:
Diện tích một mặt `(S) = a^2 = 3^2 = 9dm^2`
Thể tích `(V) = a^3 = 3^3 = 27dm^3`
b) Để S = `25dm^2`, ta cần tìm giá trị của a. Ta có:
`a^2 = 25`
=> `a = √25 = 5dm`
c) Để V = `64dm^3`, ta cần tìm giá trị của a. Ta có:
`a^3 = 64`
=> `a = ∛64 = 4dm`

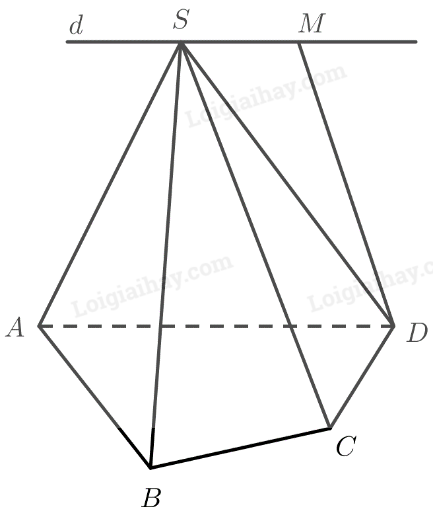
\(A{\rm{D}}M{\rm{S}}\) là hình thang có hai đáy là \(A{\rm{D}}\) và \(M{\rm{S}}\) nên \(A{\rm{D}}\parallel M{\rm{S}}\).
Theo đề bài ta lại có \(d\parallel A{\rm{D}}\).
Do đó \(d \equiv MS\) (theo định lí 1).
Lại có: \(SM \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {SA{\rm{D}}} \right)\).

Với a = 0, b = 1, hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{2x}&{{\rm{ }}x < 2}\\4&{{\rm{ }}x = 2}\\{ - 3x + 1}&{{\rm{ }}\,x > 2}\end{array}} \right.\)
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + 1} \right) = - 3.2 + 1 = - 5\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x} \right) = 2.2 = 4\\ \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)\end{array}\)
Do đó không tồn tại giới hạn \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\)
Vậy hàm số không liên tục tại x = 2.
b) Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + b} \right) = - 3.2 + b = - 6 + b\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x + a} \right) = 2.2 + a = 4 + a\\f\left( 2 \right) = 4\end{array}\)
Để hàm số liên tục tại x = 2 thì \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = f\left( 2 \right)\)
\( \Leftrightarrow - 6 + b = 4 + a = 4 \Leftrightarrow \left\{ \begin{array}{l}4 + a = 4\\ - 6 + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 10\end{array} \right.\)
Vậy với a = 0 và b = 10 thì hàm số liên tục tại x = 2.
c) Tập xác định của hàm số là: ℝ.
Với x < 2 thì \(f\left( x \right) = 2x + a\) là hàm đa thức nên liên tục.
Với x > 2 thì \(f\left( x \right) = -3x + b\) là hàm đa thức nên liên tục.
Do đó để hàm số liên tục trên ℝ thì hàm số \(f\left( x \right)\) liên tục tại x = 2.
Vậy với a = 0 và b = 10 thỏa mãn điều kiện.

Ta có: \(v\left(t\right)=s'\left(t\right)=0,5\cdot\left(4\pi t\right)'cos\left(4\pi t\right)=2\pi cos\left(4\pi t\right)\)
Vì \(-1\le cos\left(4\pi t\right)\le1\Rightarrow-2\pi\le2\pi cos\left(4\pi t\right)\le2\Leftrightarrow-2\pi\le v\left(t\right)\le2\pi\)
Vậy vận tốc cực đại của hạt là \(2\pi cm/s\)

\(v\left(t\right)=s'\left(t\right)=0,8\pi cos\left(0,8\pi t+\dfrac{\pi}{3}\right)\\ a\left(t\right)=v'\left(t\right)=-0,64\pi^2sin\left(0,8\pi t+\dfrac{\pi}{3}\right)\)
Vì:
\(v\left(t\right)=0\\ \Leftrightarrow0,8\pi cos\left(0,8\pi t+\dfrac{\pi}{3}\right)=0\\ \Leftrightarrow0,8\pi t+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi,k\in Z\\ \Leftrightarrow0,8\pi t=\dfrac{\pi}{6}+k\pi\\ \Leftrightarrow t=\dfrac{5}{24}+\dfrac{5k}{4}\)
Thời điểm vận tốc bằng 0, giá trị tuyệt đối của vật là
\(\left|a\left(\dfrac{5}{25}+\dfrac{5k}{4}\right)\right|=\left|-0,64\pi^2sin\left[0,8\pi\left(\dfrac{5}{24}+\dfrac{5k}{4}\right)+\dfrac{\pi}{3}\right]\right|\\ =0,64\pi^2\left|sin\left(\dfrac{\pi}{2}+k\pi\right)\right|\\ =0,64\pi^2\approx6,32\)
\(\Rightarrow\) Chọn C.