Cho tâm giác ABC. Về phía ngoài vẽ 3 tam giác đều ABC1,BCA1,CAB1. Chứng minh AA1,BB1,CC1 bằng nhau và đồng quy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
17 tháng 1 2018
Giả sử →A1B=k→A1C;→B1C=m→B1A;→C1A=n→C1BA1B→=kA1C→;B1C→=mB1A→;C1A→=nC1B→
Theo giả thiết ta có : →AA1+→BB1+→CC1=⃗0=>→CA1+→AB1+→BC1=⃗0=>11−k→BC+11−n→AB+11−m→CA=⃗0AA1→+BB1→+CC1→=0→=>CA1→+AB1→+BC1→=0→=>11−kBC→+11−nAB→+11−mCA→=0→
hay →BC=1−k1−m→AC+1−k1−n→BABC→=1−k1−mAC→+1−k1−nBA→
mà →BC=→BA+→ACBC→=BA→+AC→
=> 1−k1−m=1;1−k1−n=11−k1−m=1;1−k1−n=1
=> k=m=nk=m=n
Theo định lí Cê va cho 3 đường đồng quy : kmn=−1kmn=−1=>k=m=n=−1k=m=n=−1
-> A1,B1,C1 là trung điểm BC,CA,AB
-> tam giác ABC đều
S
2 tháng 9 2017
Kẻ DM ∟ AC sao cho DM = AB.
Dễ dàng chứng minh Δ DMC = Δ AEB (c - g - c)
=> ^DCM = ^AEB và BE = MC (1)
Δ BMD = Δ BED (c - g - c)
=> ^BMD = ^BED và BM = BE (2)
(1) và (2) cho:
^DCM = ^BMD và CM = MB
=> Δ BMC cân tại M
mà ^DMC + ^DCM = 90o (Δ MDC vuông)
=> ^DMC + ^BMD = 90o
=> Δ BMC vuông cân.
=> BCM = 45o
Mà ^ACB + ^DCM = ^BCM
=> ^ACB + ^AEB = 45o (vì ^AEB = ^DCM (cmt))
Cách 2:
Đặt AB = a
ta có: BD = a√2
Do DE/DB = DB/DC = 1/√2
=> Δ DBC đồng dạng Δ DEB (c - g - c)
=> ^DBC = ^DEB
Δ BDC có ^ADB góc ngoài
=> ^ADB = ^DCB + ^DBC
hay ^ACB + ^AEB = 45o
Cách 3
ta có:
tanAEB = AB/AE = 1/2
tanACB = AB/AC = 1/3
tan (AEB + ACB) = (tanAEB + tanACB)/(1 - tanAEB.tanACB)
= (1/2 + 1/3)/(1 - 1/2.1/3) = 1 = tan45o
Vậy ^ACB + ^AEB = 45o
2 tháng 9 2017
Kẻ DM ∟ AC sao cho DM = AB.
Dễ dàng chứng minh Δ DMC = Δ AEB (c - g - c)
=> ^DCM = ^AEB và BE = MC (1)
Δ BMD = Δ BED (c - g - c)
=> ^BMD = ^BED và BM = BE (2)
(1) và (2) cho:
^DCM = ^BMD và CM = MB
=> Δ BMC cân tại M
mà ^DMC + ^DCM = 90o (Δ MDC vuông)
=> ^DMC + ^BMD = 90o
=> Δ BMC vuông cân.
=> BCM = 45o
Mà ^ACB + ^DCM = ^BCM
=> ^ACB + ^AEB = 45o (vì ^AEB = ^DCM (cmt))
AA
Admin (a@olm.vn)
Admin
VIP
24 tháng 1 2020
Bạn xem ở đây nhé
Câu hỏi của Nguyễn Thị Thùy Dung - Toán lớp 9 | Học trực tuyến
AA
Admin (a@olm.vn)
Admin
VIP
24 tháng 1 2020
Bạn xem ở đây nhé.
Câu hỏi của Nguyễn Thị Thùy Dung - Toán lớp 9 | Học trực tuyến
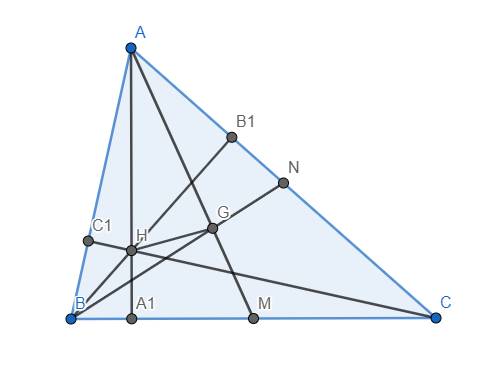
Gọi O là giao điểm của AA1 và CC1. Ta chứng minh \(\widehat{AOB}+\widehat{AOB_1}=180^o\).
Ta có: \(\Delta C_1BC=\Delta ABA_1\) vì \(C_1B=AB\), BC=BA1, góc C1BC = góc ABA1 (=góc ABC+60độ).
Suy ra \(\widehat{BC_1C}=\widehat{BAA_1}\) suy tiếp \(C_1BOA\) là tứ giác nội tiếp đường tròn.
\(\Rightarrow\widehat{AC_1B}+\widehat{AOB}=180^o\) \(\Rightarrow\widehat{AOB}=120^o\) và \(\widehat{C_1OB}=\widehat{C_1OA}=60^o\) (cùng chắn hai cung có độ dài bằng nhau).
Tương tự ta có các góc AOB1, B1OC, COA1, A1OB đều bằng 60 độ.
Suy ra \(\widehat{AOB}+\widehat{AOB_1}=180^o\)
Vậy BOB1 thẳng hàng