Trong mặt phẳng Oxy cho (P) y=mx2 và (d) y=2x+m ( m khác 0) tìm toạ độ của (d) và (P) khi m= căn 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 7 2023
a: khi m=2 thì (d): y=4x-2^2+1=4x-3
PTHĐGĐ:
x^2-4x+3=0
=>x=1 hoặc x=3
Khi x=1 thì y=1
Khi x=3 thì y=9
b: PTHĐGĐ là;
x^2-2mx+m^2-1=0
Δ=(-2m)^2-4(m^2-1)=4>0
=>(P) luôn cắt (d) tại hai điểm phân biệt
2y1+4m*x2-2m^2-3<0
=>2(2mx1-m^2+1)+4m*x2-2m^2-3<0
=>4m*x1-2m^2+2+4m*x2-2m^2-3<0
=>-4m^2+4m*(x1+x2)-1<0
=>-4m^2+4m*(2m)-1<0
=>-4m^2+8m-1<0
=>\(\left[{}\begin{matrix}m< \dfrac{2-\sqrt{3}}{2}\\m>\dfrac{2+\sqrt{3}}{2}\end{matrix}\right.\)
5 tháng 7 2023
a: Δ//d
=>Δ: 2x-y+c=0
Thay x=1 và y=-2 vào Δ, ta được:
c+2+2=0
=>c=-4
b: B thuộc d nên B(x;2x+3)
M(1;-2); A(0;3)
\(\overrightarrow{MA}=\left(-1;5\right);\overrightarrow{MB}=\left(x-1;2x+5\right)\)
ΔBAM vuông tại M
=>-1(x-1)+5(2x+5)=0
=>-x+1+10x+25=0
=>9x=-26
=>x=-26/9
=>B(-26/9;-25/9)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 5 2020
Khi \(m=5\) pt (d) có dạng: \(y=-5x-2\)
Phương trình hoành độ giao điểm (d) và (P):
\(2x^2=-5x-2\Leftrightarrow2x^2+5x+2=0\Rightarrow\left[{}\begin{matrix}x=-\frac{1}{2}\\x=-2\end{matrix}\right.\)
Với \(x=-\frac{1}{2}\Rightarrow y=2x^2=\frac{1}{2}\)
Với \(x=-2\Rightarrow y=2x^2=8\)
Vậy có 2 giao điểm: \(\left(-\frac{1}{2};\frac{1}{2}\right)\) và \(\left(-2;8\right)\)
15 tháng 4 2022
Phương trình hoành độ giao điểm là:
\(x^2-2x-m^2-m+3=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot\left(-m^2-m+3\right)\)
\(=4+4m^2+4m-12=4m^2+4m-8\)
\(=4\left(m+2\right)\left(m-1\right)\)
Để (P) tiếp xúc với (d) thì (m+2)(m-1)=0
=>m=-2(loại) hoặc m=1(nhận)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
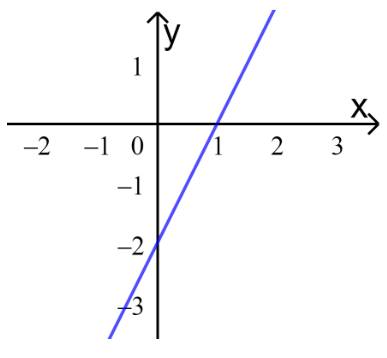
a) Cho \(x=0\Rightarrow y=-2\)
Cho \(y=0\Rightarrow x=1\)
Nối hai điểm (0;-2) và (1;0) ta được:
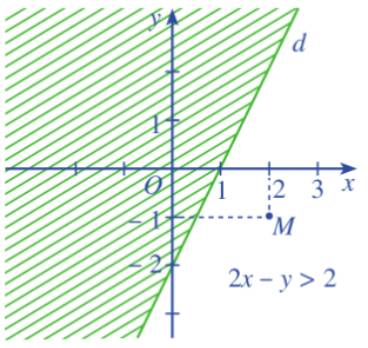
b) Thay tọa độ điểm M vào bất phương trình (3) ta được:
\(2.2 - \left( { - 1} \right) > 2 \Leftrightarrow 5 > 2\)(Luôn đúng)
Vậy (2;-1) là một nghiệm của bất phương trình (3)
c) Ta gạch đi nửa mặt phẳng không chứa M được:
AH
Akai Haruma
Giáo viên
30 tháng 4 2023
Lời giải:
PT hoành độ giao điểm:
$3x+m-2=-2x+6m+3$
$\Leftrightarrow 5x=5m+5$
$\Leftrightarrow x=m+1$
$y=3x+m-2=3(m+1)+m-2=4m+1$
Vậy tọa độ giao điểm của $(d)$ và $(d_1)$ là $I(m+1, 4m+1)$
$I$ thuộc đường tròn $(O)$ bán kính 3
Tức là $OI=3$
$\Leftrightarrow \sqrt{(m+1)^2+(4m+1)^2}=3$
Giải pt trên suy ra $m=-1$ hoặc $m=\frac{7}{17}$
25 tháng 5 2021
Xét phương trình hoành độ ta có :\(mx^2-2x+m^2=0\)
\(\Delta=b^2-4ac=4-4m^3\)
Để phương trình có nghiệm thì \(\Delta\ge0\)hay \(4-4m^3\ge0\)
\(4\ge4m^3\)
\(1\ge m^3\)
\(1\ge m\)
Theo Vi-ét ta có \(\hept{\begin{cases}xA+xB=\frac{-b}{a}=\frac{2}{m}\\xAxB=\frac{c}{a}=m\end{cases}}\)
Vì m >0 nên \(xAxB>0\)
Vậy phương trình có hai nghiệm cùng dấu nên A B nằm cùng 1 phía trục tung
Ta có :\(\frac{2}{xA+xB}+\frac{1}{4xAxB+1}\)
\(\frac{2}{\frac{2}{m}}\)\(+\frac{1}{4m+1}\)= \(m+\frac{1}{4m+1}=\frac{m\left(4m+1\right)}{4m+1}+\frac{1}{4m+1}\)=\(\frac{4m^2+m+1}{4m+1}=P\)
\(4m^2+m+1=P\left(4m+1\right)\)
\(4m^2+m+1=4mP+P\)
\(4m^2+m+1-4mP-P=0\)
\(4m^2+m-4mP+1-P=0\)
\(4m^2+m\left(1-4P\right)+1-P=0\)
\(\Delta=b^2-4ac=\left(1-4P\right)^2-16\left(1-P\right)\)
\(=1-8P+16P^2-16+16P\)
\(=-15+8P+16P^2\)
Để phương trình có nghiệm thì \(\Delta\ge0\)hay \(16P^2+8P-15\ge0\)
\(\orbr{\begin{cases}P\le\frac{-5}{4}\\P\ge\frac{3}{4}\end{cases}}\)
Vậy minP =\(\frac{3}{4}\)
Dấu = xảy ra \(< =>\)\(\frac{4m^2+m+1}{4m+1}=P\)
\(\frac{4m^2+m+1}{4m+1}=\frac{3}{4}\)
\(4\left(4m^2+m+1\right)=3\left(4m+1\right)\)
\(16m^2+4m+4-12m-3=0\)
\(16m^2-8m+1=0\)
\(m=\frac{1}{4}\)
Vậy minP=\(\frac{3}{4}\)khi và chỉ khi \(m=\frac{1}{4}\)