Cho \(\Delta ABC\) cân tại A. Đường cao AI.Từ AI kẻ \(IM\perp AB\)tại M.\(IN\perp AC\)tại N.
a,Chứng minh I là trung điểm của BC
b,\(\Delta AMN\)cân tại A
c.Vẽ K sao cho I là trung điểm của NK.Chứng minh BC là đường trung trực KM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét △AMD và △DMC
AB=AC(giả thuyết)
Cạnh AM là cạnh chung
BM= CM ( M là trung điểm của cạnh BC)
=> △AMD=△DMC
Sorry bạn nhé mk chỉ bt làm câu a thui ☹

a/ Xét \(\Delta ABC\) và \(\Delta HAC\) có :
\(\left\{{}\begin{matrix}\widehat{C}chung\\\widehat{BAC}=\widehat{AHC}=90^0\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\sim HAC\left(g-g\right)\)
b/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=4,8cm\)
c/ \(\Delta HEA\sim\Delta CEH\left(g-g\right)\)
\(\Leftrightarrow\dfrac{HE}{CE}=\dfrac{EA}{HE}\Leftrightarrow HE^2=EA.EC\left(đpcm\right)\)

a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)

c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)

d) ΔEAD ∼ ΔBAC

ΔABC vuông tại A, theo định lí Pytago:

Theo b, ta có:
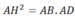



a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật

a: Xét ΔABH vuông tai H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: Xét ΔABC co
AH,CN là trung tuyến
AH cắt CN tại G
=>G là trọng tâm
c: Xét ΔABC có
H là trung điểm của CB
HE//AB
=>E là trung điểm của AC
=>B,G,E thẳng hàng

câu a theo hình của mình thì làm được rồi nhưng câu b mtheo hình của mình thì lại thấy kì kì bạn thử vẽ hình hộ mình được không
a) Xét ΔADI và ΔAHI , có :
ID = IH ( I là trung điểm của DH )
IA chung
góc AID = góc AIH = 90o
=> ΔADI = ΔAHI (c.g.c)

Xét ∆ABC vuông tại A, theo định lý Pytago ta có:
(BC)²=(AB)²+(AC)²
15²=9²+AC² suy ra AC=12
Do 9<12<15suy ra AB<AC<BC
Suy ra BÂC<ABC<BÂC
b)xét ,∆IMC và ∆INB
IC=IB(do AI là đường trung tuyến ∆ABC)
IM=IN(gt);CIM=BIN(đd)suy ra ∆IMC=∆INB(c-g-c)
ICM=IBN(2g tương ứng) mà 2 góc này ở vị trí sole trong suy ra CM//BN kéo dài AC//BN
C) Ta có AI là trung tuyến của ∆ABC vuông tại A(1)có AI ứng với BC mà BC là cạnh huyền
Suy ra AI=½BC=IC suy ra AI=IC suy ra ∆AIC cân tại I
Xét trong ∆AIC cân, có IM là đường cao suy ra IM là đường trung trực ∆AIC suy ra MA=MCsuy ra BM là đường trung tuyến ∆ABC(2)
Từ (1)và(2) ta có :
AI và BM là 2 đường trung tuyến của∆ABC cắt nhau tại G suy ra G là trọng tâm của ∆ABC
Ta có :½ BC+½AC=½.27 =27/2 suy ra BI+AM=27/2
Xét BM và BI ta có : BM>AB( QH giữa đường vuông góc và đường xiên)suy ra 12<BM(1)
BI=BC/2=15/2<12(2)
Từ (1)và (2) ta có: BI<12<BM suy ra BI<BM(3)
Xét ∆AIM vuông tại M có AI là cạnh huyền; AM là cạnh góc vuông
Suy ra:AM<AI(4)
Từ (3)và (4) ta có
BM+AI>BI+AM=27/2
Suy ra BM+AI>27/2
a) xét 2 tam giác vuông AIB và AIC có:
AI cạnh chung
AB=AC(gt)
=> tam giác AIB=tam giác AIC(cạnh huyền-cạnh góc vuông)
=> IB=IC=> I là trung điểm của BC
b) xét 2 tam giác vuông MIB và NIC có:
IB=IC(theo câu a)
\(\widehat{B}\)=\(\widehat{C}\)(gt)
=> tam giác MIB =tam giác NIC(CH-GN)
=> MB=NC mà AB=AC=> AM=AN
=> tam giác AMN cân tại A
c)