Trong mặt phẳng Oxy, cho đường tròn (c) có phương trình \(x^2+y^2-4x-y-83=0\) và đường thẳng d: x + 2y + 20 = 0. Viết phương trình đường thẳng Δ song song với đường thẳng d và cắt đường tròn C tạo thành một dây cung có độ dài lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(d')//(d)
=>(d'): 4x-3y+c=0
(C): x^2-4x+4+y^2+6y+9-16=0
=>(x-2)^2+(y+3)^2=16
=>R=4; I(2;-3)
Theo đề, ta có: d(I;(d'))=4
=>\(\dfrac{\left|2\cdot4+\left(-3\right)\cdot\left(-3\right)+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=4\)
=>|c+17|=4*5=20
=>c=3 hoặc c=-37

a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6

1.
\(\left(C\right):x^2+y^2-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)
Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)
Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)
Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)
\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)
\(\Leftrightarrow m=-1\pm\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)
2.
Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)
Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)
\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)
\(\Leftrightarrow m=-1\pm2\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)

Đáp án C
- Đường thẳng d’ song song với d nên có dạng: 3x+ y+ m= 0
- IH là khoảng cách từ I đến d’:
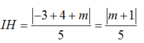
- Xét tam giác vuông IHB:

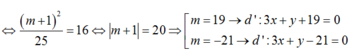

1: Gọi I(0,y) là tâm cần tìm
Theo đề, ta có: IA=IB
=>\(\left(0-3\right)^2+\left(5-y\right)^2=\left(1-0\right)^2+\left(-7-y\right)^2\)
=>y^2-10y+25+9=y^2+14y+49+1
=>-10y+34=14y+50
=>-4y=16
=>y=-4
=>I(0;-4)
=>(x-0)^2+(y+4)^2=IA^2=90
2: Gọi (d1) là đường thẳng cần tìm
Vì (d1)//(d) nên (d1): 4x+3y+c=0
Theo đề, ta có: d(I;(d1))=3 căn 10
=>\(\dfrac{\left|0\cdot4+\left(-4\right)\cdot3+c\right|}{5}=3\sqrt{10}\)
=>|c-12|=15căn 10
=>\(\left[{}\begin{matrix}c=15\sqrt{10}+12\\c=-15\sqrt{10}+12\end{matrix}\right.\)

(C): (x-1)^2+(y+2)^2=4
=>R=2; I(1;-2)
Vì (d)//Δ nên (d): 4x-3y+c=0
\(d\left(I;\left(d\right)\right)=2\)
=>\(\dfrac{\left|1\cdot4+\left(-2\right)\cdot\left(-3\right)+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=2\)
=>|c+4+6|=10
=>|c+10|=10
=>c=0 hoặc c=-20
=>4x-3y=0 hoặc 4x-3y-20=0
\(\left(C\right)\) có tâm \(I\left(2;\frac{1}{2}\right)\)
Trong đường tròn, dây cung có độ dài lớn nhất khi và chỉ khi nó là đường kính \(\Rightarrow\Delta\) đi qua I
Do \(\Delta//d\) nên \(\Delta\) có 1 vtpt \(\overrightarrow{n_{\Delta}}=\left(1;2\right)\)
Phương trình \(\Delta\):
\(1\left(x-2\right)+2\left(y-\frac{1}{2}\right)=0\Leftrightarrow x+2y-3=0\)