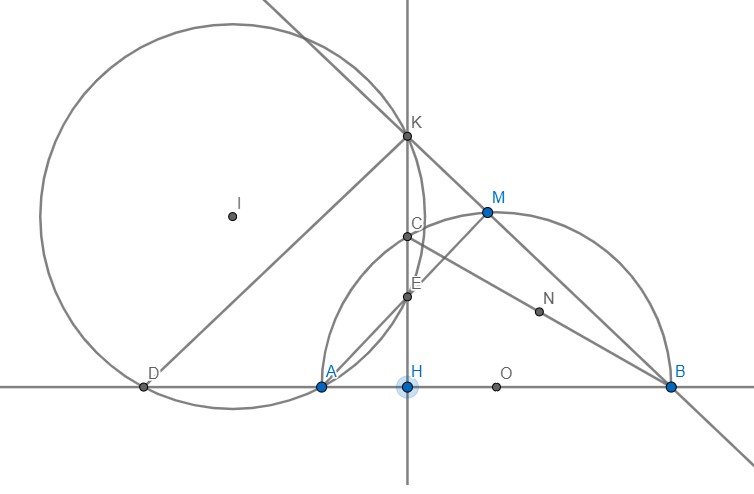
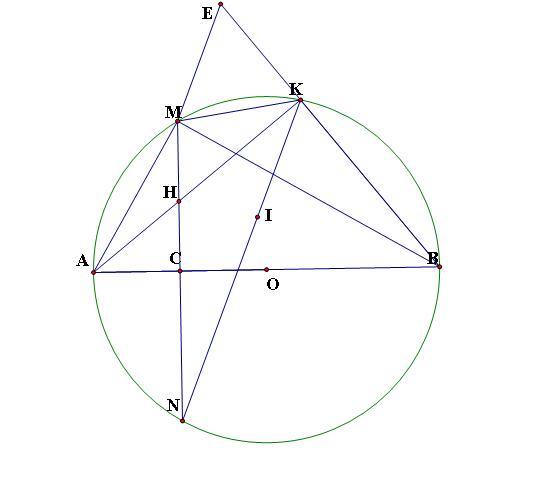
1. cho nửa đường tròn tâm o , đường kính ab = 2r . gọi c là trung điểm của oa . qua c kẻ đường thẳng vuông góc với oa cắt đường tròn đó tại 2 điểm phân biệt m và n . trên cung nhỏ bm lấy điểm k ( k khác b và m ) , trên tia kn lấy điểm I sao cho ki = kn . gọi h là giao điểm của ak và mn . c/m :
a. tứ giác bchk nội tiếp ưb.
b. tính ak . ah theo r
c. chứng tỏ : ni = bk