Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: góc AKP = 90độ ( Góc nội tiếp chắn nửa đường tròn)
Mà AK giao MN tại H =) Góc HKP = 90độ (1)
Lại có: MC vuông góc AB =) Góc HCB = 90độ (2)
Từ (1) và (2) =) góc HKP + góc HCP = 180độ
Mà 2 góc đối nhau
=) Tứ giác BCHK nội tiếp

a.
Góc AKB là góc nội tiếp chắn nửa (O) nên ∠AKB=90o∠AKB=90o
Khi này dễ dàng có đpcm
b.
Do C là trung điểm OA nên AC=OA2=R2AC=OA2=R2
Tứ giác BCHK nội tiếp nên chứng minh được △AHC∼△ABK△AHC∼△ABK
Từ đó: ACAK=AHAB⇒AH.AK=AC.AB=R2.2R=R2ACAK=AHAB⇒AH.AK=AC.AB=R2.2R=R2
c.
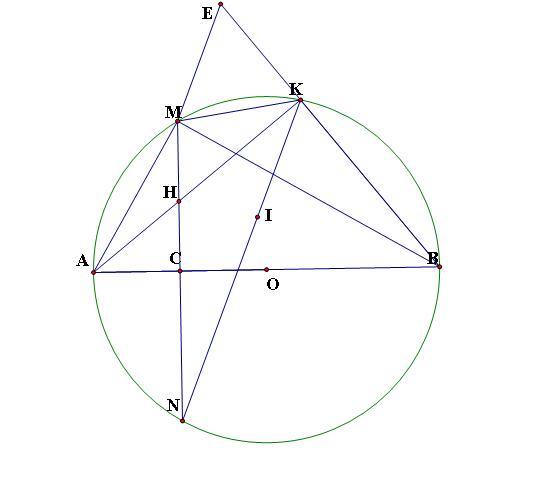
Lấy điểm E trên tia đối của BK sao cho KE=KM=KI
Chứng minh được tam giác AMO đều (có 3 cạnh = nhau) khi đó ∠MAB=60o∠MAB=60o
Dễ dàng chứng minh được tứ giác ABKM nội tiếp nên ∠MKE=∠MAB=60o∠MKE=∠MAB=60o
khi đó tam giác MKE đều nên ME = MK(1)
Có ∠CMB=∠MAB=6oo∠CMB=∠MAB=6oo (hai góc cùng phụ với góc AMC) nên
∠MNK=∠BME(2)∠MNK=∠BME(2)
Góc CMB=60oCMB=60o nên MB=2MCMB=2MC mà MN=2MCMN=2MC nên MN=MB(3)MN=MB(3)
Từ (1),(2) và (3) nên △NMK=△BME△NMK=△BME nên NK=BENK=BE hay NI+IK=BK+KINI+IK=BK+KI từ đó có đpcm
Hình gửi kèm

a: góc AKB=1/2*180=90 độ
góc HCB+góc HKB=180 độ
=>BKHC nội tiếp
b: Xét ΔACH vuông tại C và ΔAKB vuông tại K có
góc CAH chug
=>ΔACH đồng dạng với ΔAKB
=>AC/AK=AH/AB
=>AK*AH=AC*AB=1/2R*2R=R^2

a: góc AKB=1/2*sđ cung AB=90 độ
góc HCB+góc HKB=180 độ
=>HCBK nội tiếp
b: Xét ΔACH vuông tại C và ΔAKB vuông tại K có
góc CAH chung
=>ΔACH đồng dạng với ΔAKB
=>AC/AK=AH/AB
=>AK*AH=AB*AC=2R*1/2R=R^2

Cần nắm:+Cái này chỉ áp dụng cho viet
1)x12+x22=(x1+x2)2-2x1x2 ( cái này cần nắm chắc 100% ra thi ok)
2)x13+x23=(x1+x2)3-3x1x2(x1+x2)
3)\(\frac{1}{x_1}+\frac{1}{x_2}=\frac{x_1+x_2}{x_1x_2}\)
+)cần nhớ hệ thức viet
+)phải biết giải pt làm sao cho nó gọn nhất để giải
Nếu giải bài toán dạng này thì cần trải qua những bước sau (đây là nhưng bài thông thường gặp dạng khác tự lực cánh sinh)
*ở đây có thể có câu c/m pt có nghiệm hay nghiệm phân biệt với mọi m nên t làm lun
Nên nhớ pt có 2 nghiệm phân biệt thìΔ>0, có nghiệm thì chỉ cần Δ\(\ge\)0
pt:x2-2(m-1)x-4m=0
Đây là thí dụ nha!
c/m pt lun có nghiệm
b1)biến đổi : ở đây biến đổi giải theoΔ hay Δ' gì cũng được
x2-2(m-1)x-4m=0 (a=1, b'=-(m-1), c=-4m)
Δ'=b'2-ac=(m-1)2+4m ( để pt này có nghiệm thì ta c/m Δ\(\ge\)0 nha còn nếu người ta yêu cầu khác thì tuỳ)
-biến đổi thêm chớ bây nhiêu chưa được:Δ'=m2-2m+1+4m
=>Δ=m2+2m+1 và biến rút gọn thành (m+1)2
rồi ở đây NHỚ dùm cái là bất cứ cái j thì khi nó bình phương lên thi lun≥0 từ đó tự kết luận
tìm m để pt có 2 nghiệm x1và x2 thoả mãn: x12+x22-x1-x2=6
+)cái này trước tiên thì cần phải chứng minh được rằng pt có nghiệm cái đã vì khi nó vô nghiệm thi làm sao thoả mãn biểu thức
+)tt mày cần biến đổi cái biểu thức trên và áp dụng cái cần nhớ t nói ở đầu bài
+)theo cái hệ thức viet nữa , giải xong biểu thức nữa thì ráp vào
NHÌN ANH LÀM Rồi BẮT CHƯỚC
+) \(\left\{{}\begin{matrix}x_1+x_2=-\frac{b}{a}=2\left(m-1\right)\\x_1x_2=\frac{c}{a}=-4m\end{matrix}\right.\)
+)x12+x22-x1-x2=6 ( ở đây mày thấy x1-x2ko nên ta ko ráp viet vào được nên biến đổi nó)
(x1+x2)2-2x1x2-(x1+x2) ( đố thấy chưa chỉ cần đóng ngoặc thì dấu trong ngoặc đỏi ko nhơ thì lên mạng tra t mệt r)
Rùi giờ tới đây là ráp ok mày nhìn ở cái viet và cái biểu thức vừa r chổ nào giống thì thay vô
\(\left[2\left(m-1\right)\right]^2\)\(-2\left(-4m\right)\)\(-\left[2\left(m-1\right)\right]\)=6
(2m-2)2+8m-2m-2=6
4m2-8m+4+8m-2m+2=6
4m2-2m=0 =>2m(2m-1)=0
=>\(\left\{{}\begin{matrix}2m=0\\2m-1=0\end{matrix}\right.< =>\left\{{}\begin{matrix}m=0\\m=\frac{1}{2}\end{matrix}\right.\)
Kết luận