Xét hàm số f(x) liên tục trên đoạn R, thỏa mãn đk (x+2)f(x)+(x+1)f'(x)=ex và f(0)=1/2. tính f(2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
14 tháng 11 2018
Chọn A
![]() .
.
Nhân 2 vế của ![]() với
với ![]() ta được
ta được ![]() .
.
Hay ![]() .
.
Xét ![]() .
.
Đặt ![]() .
.
![]()
Suy ra ![]() .
.
Theo giả thiết ![]() nên
nên ![]()
![]() .
.

CM
13 tháng 9 2018
Chọn đáp án C.
Lấy tích phân hai vế trên đoạn [0;2] có
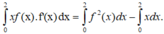
Tích phân từng phần có
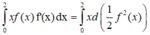
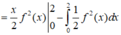
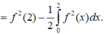
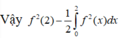
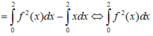
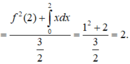
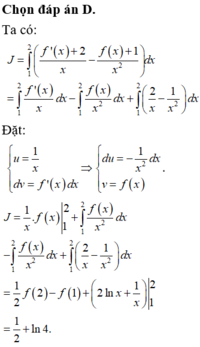

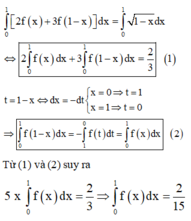
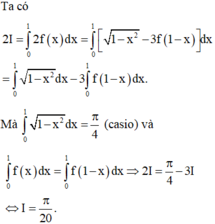

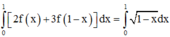
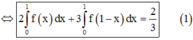
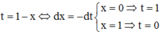
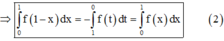
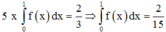
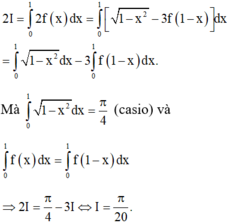


\(\left(x+2\right)f\left(x\right)+\left(x+1\right)f'\left(x\right)=e^x\)
\(\Leftrightarrow e^x\left(x+2\right)f\left(x\right)+e^x\left(x+1\right)f'\left(x\right)=e^{2x}\)
\(\Leftrightarrow\left[e^x\left(x+1\right).f\left(x\right)\right]'=e^{2x}\)
Lấy nguyên hàm 2 vế:
\(\Leftrightarrow e^x\left(x+1\right).f\left(x\right)=\int e^{2x}dx=\frac{1}{2}e^{2x}+C\)
Do \(f\left(0\right)=\frac{1}{2}\Rightarrow e^0\left(0+1\right).f\left(0\right)=\frac{1}{2}e^0+C\Rightarrow C=0\)
\(\Rightarrow e^x\left(x+1\right)f\left(x\right)=\frac{1}{2}e^{2x}\Rightarrow f\left(x\right)=\frac{e^{2x}}{2e^x\left(x+1\right)}=\frac{e^x}{2\left(x+1\right)}\)
\(\Rightarrow f\left(2\right)=\frac{e^2}{6}\)