cho tam giác abc . các đường trung tuyến AM , AB , CF cắt nhau tại G
A, So sánh GN với GB , GN vs BN , GB vs BN
b, tính tỉ số \(\frac{\text{diện tích tam giác ABG }}{\text{diện tích tam giác ABM }}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

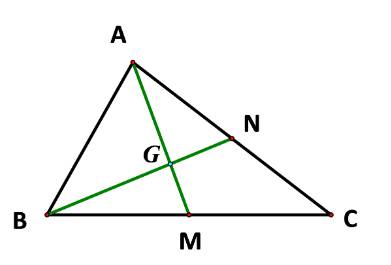
Ta có: \(\overrightarrow {AG} ,\overrightarrow {AM} \)là hai vecto cùng hướng và \(\left| {\overrightarrow {AG} } \right| = \frac{2}{3}\left| {\overrightarrow {AM} } \right|\)
Suy ra \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} .\) Vậy \(a = \frac{2}{3}.\)
Ta có: \(\overrightarrow {GN} ,\overrightarrow {GB} \)là hai vecto ngược hướng và \[\left| {\overrightarrow {GN} } \right| = \frac{1}{3}BN = \frac{1}{2}.\left( {\frac{2}{3}BN} \right) = \frac{1}{2}\left| {\overrightarrow {GB} } \right|\]
Suy ra \(\overrightarrow {GN} = - \frac{1}{2}\overrightarrow {GB} .\) Vậy \(b = - \frac{1}{2}.\)

a: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
M là trung điểm của GB
N là trung điểm của GC
Do đó: MN là đường trung bình của ΔGBC
Suy ra:MN//BC và \(MN=\dfrac{BC}{2}\)(2)
Từ (1) và (2) suy ra DE//MN và DE=MN
b:Xét ΔEBC và ΔDCB có
EB=DC
\(\widehat{EBC}=\widehat{DCB}\)
BC chung
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{ECB}=\widehat{DBC}\)
hay \(\widehat{GBC}=\widehat{GCB}\)
Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)
nên ΔGBC cân tại G
Suy ra: GB=GC
Suy ra: G nằm trên đường trung trực của BC(3)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(4)
Từ (3) và (4) suy ra AG là đường trung trực của BC
hay AG\(\perp\)BC

a: Xét ΔABC có
CM là trung tuyến
BN là trung tuyến
CM cắt BN tại G
Do đó: G là trọng tâm của ΔABC
=>AG là đường trung tuyến
mà P là trung điểm của BC
nên A,G,P thẳng hàng
b: GA=2/3AP
GB=2/3BN
GC=2/3CM
c: GM=1/2GC
GN=1/2GB
GP=1/2GA
a, do 3 đường trung tuyến cắt nhau tại G
=> G là trọng tâm
=> GN=1/2 BG
GN=1/3 BN
GB=2/3BN
câu b em có ghi nhầm đề ko vậy
hok tốt
nếu sai gửi qua ib nha