Cho hàm số y=\(\frac{1}{3}\)x3 -\(\frac{\left(3m+2\right)x^2}{2}\) +(2m2 +3m +1)x + m- 2 (1). Gọi S là tâp hợp tất cả các giá trị của tham số m sao cho hàm số (1) đạt cực đại, cực tiểu tại xCĐ, xCT sao cho 3x2CĐ = 4xCT. Khi đó tổng các phần tử của tập S =?
A. S=\(\frac{-4-\sqrt{7}}{6}\)
B. S=\(\frac{4+\sqrt{7}}{6}\)
C. S=\(\frac{-4+\sqrt{7}}{6}\)
D. S=\(\frac{4-\sqrt{7}}{6}\)



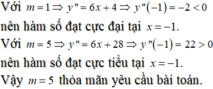
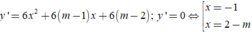
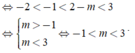
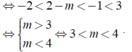
\(y'=x^2-\left(3m+2\right)x+2m^2+3m+1\)
\(\Delta=\left(3m+2\right)^2-4\left(2m^2+3m+1\right)=m^2\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\frac{3m+2+m}{2}=2m+1\\x_2=\frac{3m+2-m}{2}=m+1\end{matrix}\right.\)
Để hàm số có cực đại, cực tiểu \(\Rightarrow x_1\ne x_2\Rightarrow m\ne0\)
- Nếu \(m>0\Rightarrow2m+1>m+1\Rightarrow\left\{{}\begin{matrix}x_{CĐ}=m+1\\x_{CT}=2m+1\end{matrix}\right.\)
\(\Rightarrow3\left(m+1\right)^2=4\left(2m+1\right)\) \(\Rightarrow3m^2-2m-1=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-\frac{1}{3}< 0\left(l\right)\end{matrix}\right.\)
- Nếu \(m< 0\Rightarrow m+1>2m+1\Rightarrow\left\{{}\begin{matrix}x_{CĐ}=2m+1\\x_{CT}=m+1\end{matrix}\right.\)
\(\Rightarrow3\left(2m+1\right)^2=4\left(m+1\right)\Rightarrow12m^2+8m-1=0\)
\(\Rightarrow\left[{}\begin{matrix}m=\frac{-2+\sqrt{7}}{6}>0\left(l\right)\\m=\frac{-2-\sqrt{7}}{6}\end{matrix}\right.\) \(\Rightarrow\sum m=\frac{4-\sqrt{7}}{6}\)