giải theo góc cạnh góc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 11 2017
A B C H
Xét \(\Delta AHB\)và \(\Delta AHC\)
AH cạnh chung
\(\widehat{AHB}=\widehat{AHC}\)( kề bù )
\(\widehat{B}=\widehat{C}\) ( đề bài cho góc B = góc C )
\(\Rightarrow\)\(\Delta AHB=\Delta AHC\)( g - c - g )
\(\Rightarrow\)\(AB=AC\)( 2 cạnh tương ứng bằng nhau )
bài này phải vễ thêm yếu tố phụ là AH nha
L
25 tháng 11 2020
- Giả sử tam giác ABC vuông tại A . Theo bài ra , ta có :
\(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\left(1\right)\)
- Áp dụng đlí Py - ta - go cho tam giác vuông ABC ( \(\widehat{A}=90^o\))
Ta có : \(BC^2=AB^2+AC^2\)
\(\Leftrightarrow125^2=\left(\frac{3}{4}AC\right)^2+AC^2\)
\(\Leftrightarrow15625=\frac{9}{16}AC^2+AC^2\)
\(\Leftrightarrow15625=\left(\frac{9}{16}+1\right)AC^2\)
\(\Leftrightarrow\frac{25}{16}AC^2=15625\)
\(\Leftrightarrow AC^2=\frac{15625.16}{25}\)
\(\Leftrightarrow AC=\sqrt{\frac{15625.16}{25}}=\frac{125.4}{5}=100\left(cm\right)\)
Thay AC = 100cm vào (1) , ta được :
\(AB=\frac{3}{4}.100=75\left(cm\right)\)
- Áp dụng hệ thức lượng trong tam giác ABC ( \(\widehat{A}=90^o\)) đường cao AH , ta có :
\(AB^2=BH.BC\)
\(\Leftrightarrow BH=\frac{AB^2}{BC}=\frac{75^2}{125}=45\left(cm\right)\)
Ta lại có : BC = BH + HC
125 = 45 + HC
HC = 125 - 45 = 80 ( cm )
Vậy : AB = 75 cm
AC = 100 cm
HC = 80 cm
BH = 45 cm
19 tháng 11 2016
A B C N M
Vì \(AB=BC\)
\(\Rightarrow ABC\) là tam giác cân
Vậy \(\widehat{B}=\widehat{C}\)
Xét \(\Delta MBC\) và \(\Delta NBC\) có :
\(MB=NC\)
\(BC\) là cạnh chung
\(\widehat{B}=\widehat{C}\)
Do đó : 2 tam giác bằng nhau ( c . g . c )
NV
Nguyễn Việt Dũng
CTVVIP
22 tháng 8 2023
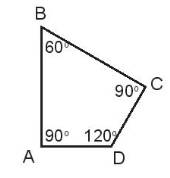
Góc | Số đo góc |
Góc đỉnh A; cạnh AB, AD | 90o |
Góc đỉnh B; cạnh BA, BC | 60o |
Góc đỉnh C; cạnh CB, CD | 90o |
Góc đỉnh D, cạnh DA, DC | 120o |
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) \(PQ = n.\cos a,PQ = m.\cos b\)
b) \(MQ = n.\sin a,PN = m.\sin b \Rightarrow MN = n.\sin a + m.\sin b\)
\(\begin{array}{l}{S_{MPQ}} = \frac{1}{2}m.\cos b.n.\sin a = \frac{1}{2}m.n.\cos b.\sin a\\{S_{NPQ}} = \frac{1}{2}n.\cos a.m.\sin b = \frac{1}{2}m.n.\cos a.\sin b\\{S_{MNP}} = \frac{1}{2}m.n.\sin \left( {a + b} \right)\end{array}\)
c) \({S_{MNP}} = {S_{MPQ}} + {S_{NPQ}} \Rightarrow \frac{1}{2}m.n.\cos b.\sin a + \frac{1}{2}m.n.\cos a.\sin b = \frac{1}{2}m.n.\sin \left( {a + b} \right)\)
\( \Rightarrow \sin \left( {a + b} \right) = \sin a.\cos b + \cos a.\sin b\)
d) \(\sin \left( {a - b} \right) = \sin \left[ {a + \left( { - b} \right)} \right] = \sin a.\cos \left( { - b} \right) + \cos a.\sin \left( { - b} \right) = \sin a.\cos b - \cos a.\sin b\)
CM
13 tháng 4 2018
sinB = b/a; cosB = c/a; tgB = b/c; cotgB = c/b
sinC = c/a; cosC = b/a; tgC = c/b; cotgB = b/c
a) b = a.(b/a) = a.sinB = a.cosC
c = a. (c/a) = a.cosB = a.sinC
b) b = c. (b/c) = c.tgB = c.cotgC
c = b.(c/b) = b.cotgB = b.tgC