cho tam giác ABC.Trên tia đối của tia AB lấy điểm E sao cho AE=2AB.Trên tia đối của tia BC lấy điểm D sao cho BD=BC. C/m BE+CF>3/2EC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có: Góc BAE + BAD = góc BCF + BCA (=180 độ)
Góc BAD = BCA
⇒ góc BAE = FCB
Xét △BAE và △FCB có:
AB = CF
BAE = FCB
AE = CB
⇒△BAE = △FCB (c.g.c)
⇒EBA = CFB
Mà góc CFB + ABF = 90 độ ⇒EBA + ABF = 90 độ
⇒ góc EBF = 90 độ ⇒BE vuông góc với BF

a) Ta có AD = AB và AE = CD. Vì AD = AB, nên tam giác ABD là tam giác cân tại A. Tương tự, tam giác AEC là tam giác cân tại A. Do đó, ta có ∠ABD = ∠BAD và ∠CAE = ∠EAC. Vì ∠BAD = ∠CAE, nên ∠ABD = ∠EAC. Vì tam giác ABD và tam giác AEC là tam giác cân tại A, nên ta có BD = AB và CE = AE. Do đó, ta có BD = AB = AE = CE. b) Ta có BD = AB và CE = AE. Vì BD = AB và CE = AE, nên ta có BD = CE. Vì BD = CE, nên tam giác BCD là tam giác cân tại B. Vì tam giác BCD là tam giác cân tại B, nên ta có ∠BCD = ∠CBD. Vì ∠BCD = ∠CBD, nên ∠BCD + ∠CBD = 180°. Do đó, ta có ∠BCD + ∠CBD = 180°. Vì ∠BCD + ∠CBD = 180°, nên tam giác BCD là tam giác đều. Vì tam giác BCD là tam giác đều, nên ta có BE = CD. c) Gọi M là trung điểm của BE và N là trung điểm của CD. Vì M là trung điểm của BE, nên ta có BM = ME. Vì N là trung điểm của CD, nên ta có CN = ND. Vì BM = ME và CN = ND, nên ta có BM + CN = ME + ND. Do đó, ta có BM + CN = ME + ND. Vì BM + CN = ME + ND, nên ta có BN = MD. Vì BN = MD, nên tam giác BMD là tam giác cân tại B. Vì tam giác BMD là tam giác cân tại B, nên ta có ∠BMD = ∠BDM. Vì ∠BMD = ∠BDM, nên ∠BMD + ∠BDM = 180°. Do đó, ta có ∠BMD + ∠BDM = 180°. Vì ∠BMD + ∠BDM = 180°, nên tam giác BMD là tam giác đều. Vì tam giác BMD là tam giác đều, nên ta có BM = MD. Vì BM = MD, nên ta có BM = MD = AM. Vậy ta có AM = AN.

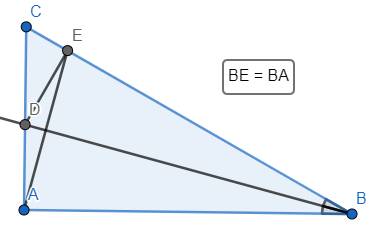
a) Xét ΔABD và ΔEBD có:
- BE = BA (giả thuyết)
- \(\widehat{ABD}=\widehat{EBD}\) (vì BD là tia phân giác của \(\widehat{ABC}\) )
- BD là cạnh chung
Suy ra ΔABD = ΔEBD (c.g.c)
b) Từ a) suy ra DE = AD (vì hai cạnh tương ứng) và \(\widehat{BAD}=\widehat{BED}=90^o\) (vì hai góc tương ứng), hay \(DE\perp BC\)
c) Từ BE = BA và DE = AD suy ra B và D đều nằm trên đường trung trực của AE, hay BD là đường trung trực của AE
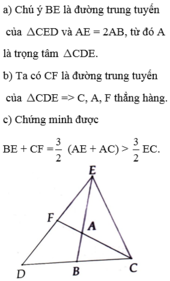
giúp mình với