cho tam giác ABC vuông tại A và AB < AC . kẻ AH vuông góc với BC tại H . trên tia đối của tia HA lấy điểm M sao cho HM = HA .a) c/m CA = CM b) c/m tam giác ABC = tam giác MBC , từ đó suy ra CB là tia phân giác của góc ACM c) tia phân giác của góc HAC cắt HC tại O . c/m MO là tia phân giác của AMC .d) từ O kẻ đường thẳng vuông góc với BC , cắt AC ở E . c/m rằng đương thẳng BE đi qua trọng tâm của tam giác...
Đọc tiếp
cho tam giác ABC vuông tại A và AB < AC . kẻ AH vuông góc với BC tại H . trên tia đối của tia HA lấy điểm M sao cho HM = HA .
a) c/m CA = CM
b) c/m tam giác ABC = tam giác MBC , từ đó suy ra CB là tia phân giác của góc ACM
c) tia phân giác của góc HAC cắt HC tại O . c/m MO là tia phân giác của AMC .
d) từ O kẻ đường thẳng vuông góc với BC , cắt AC ở E . c/m rằng đương thẳng BE đi qua trọng tâm của tam giác ABO.
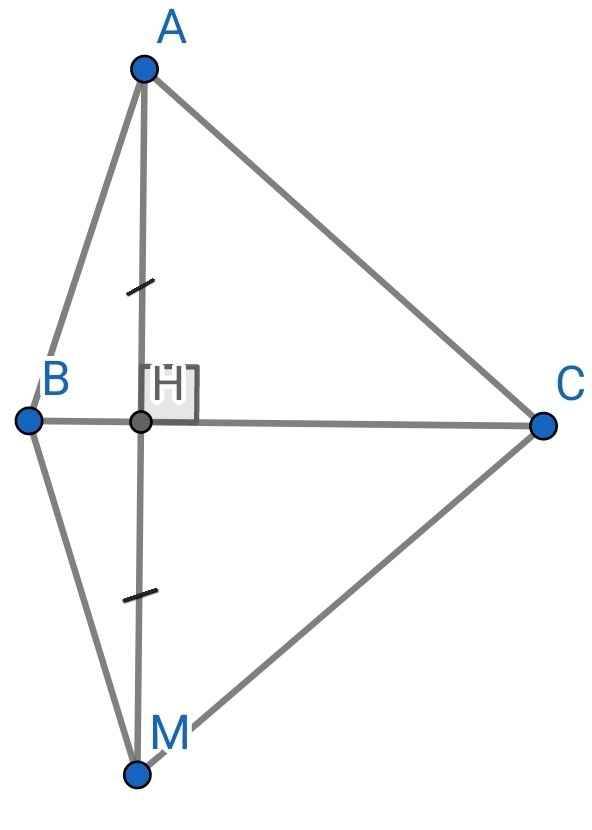
tự vẽ hình nha
a)xét tam giac ACH và tam giac MCH có:
AH=HM (gt)
góc AHC = góc MHC =90 độ
HC chung
suy ra tam giac ACH=tam giac MCH (c.g.c)
suy ra CA=CM(2 góc tương ứng)
b) ta có:tam giac AHC =tam giac MCH(theo câu a)
suy ra góc ACH = góc MCH ( 2 góc tương ứng)
suy ra CB là tia phân giác góc ACM
hay góc ACB =góc MCB (1)
xét tam giac ABC và tam giac MBC có:
AC=MC ( theo câu a)
góc ACB = góc MCB (theo (1))
BC chung
suy ra :tam giac ABC = tam giac MBC (c.g.c)
c,d tự làm.