cho hàm số (P):y=ax2 (a khác 0)
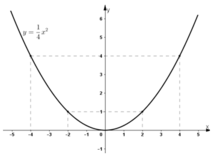
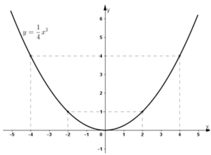
a) xác định hàm số (P). Biết rằng đồ thị của nó qua A(2;-2). Vẽ (P) với a vừa tìm.
b/ lập phương trình đ.ường thẳng (D). Biết rằng đồ thị của nó song song với đường thẳng y=2x và tiếp xúc với(P)
c/ Tìm những điểm trên (P) :y=x2 cách đều hai trục tọa độ

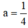
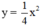
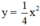
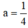
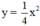
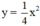
a, thay x=2, y=-2 vào y=ax^2 ta đc
-2=a*2^2
-2=4a
a=-1/2
phương trình trở thành
y=-1/2x^2
lập bảng vs x có 5 gt: -2;-1;0;1;2
tìm y theo x
kẻ đc bảng
b,gọi phương trình đường thẳng D là y=ax+b
do D song song với đường thẳng y=2x nên ta được:
a=2 và b khác 0
thay a=2 pt D trở thành
y=2x+b
do D tiếp xúc vs P nên ta đc
-1/2x^2=2x+b
-1/2x^2-2x-b=0
ta có: đenta'=1-b/2
mà D tiếp xúc vs P nên đenta' =0
1-b/2=0
b=2
vậy (D):y=2x+2