tìm x,y biét:(x-0,5)^2010+|x+y+0,5|=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(\left(x-0,5\right)^2+\left(y+0,25\right)^2=0\)
\(\Leftrightarrow x-0,5=y+0,25=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0,5\\y=-0,25\end{matrix}\right.\)

\(\left(x-0,5\right)^2+\left(y+0,25\right)^2=0\)
Do \(\hept{\begin{cases}\left(x-0,5\right)^2\ge0\\\left(y+0,25\right)^2\ge0\end{cases}\Rightarrow VT\ge0}\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x-0,5=0\\y+0,25=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=0,5\\y=-0,25\end{cases}}}\)
Vậy \(\hept{\begin{cases}x=0,5\\y=-0,25\end{cases}}\)
vì \(\hept{\begin{cases}\left(x-0,5\right)^2\ge0\\\left(y+0,25\right)\ge0\end{cases}}\)
mà \(\left(x-0,25\right)^2+\left(y-0,25\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}\left(x+0,5\right)^2=0\\\left(y-0,25\right)^2=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x+0,5=0\\y-0,25=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=-0,5\\y=0,25\end{cases}}\)

Xét hàm số g(x) = f(x) − f(x + 0,5)
Ta có
g(0) = f(0) − f(0 + 0,5) = f(0) − f(0,5)
g(0,5) = f(0,5) − f(0,5 + 0,5) = f(0,5) − f(1) = f(0,5) − f(0)
(vì theo giả thiết f(0) = f(1)).
Do đó,
g ( 0 ) . g ( 0 , 5 ) = [ f ( 0 ) − f ( 0 , 5 ) ] . [ f ( 0 , 5 ) − f ( 0 ) ] = − f ( 0 ) − f ( 0 , 5 ) 2 ≤ 0 .
- Nếu g(0).g(0,5) = 0 thì x = 0 hay x=0,5 là nghiệm của phương trình g(x) = 0
- Nếu g(0).g(0,5) < 0 (1)
Vì y = f(x) và y = f(x + 0,5) đều liên tục trên đoạn [0; 1] nên hàm số y = g(x) cũng liên tục trên [0; 1] và do đó nó liên tục trên [0; 0,5] (2)
Từ (1) và (2) suy ra phương trình g(x) = 0 có ít nhất một nghiệm trong khoảng
Kết luận : Phương trình g(x) = 0 hay f(x) − f(x + 0,5) = 0 luôn có nghiệm trong đoạn (0;0,5)


Vẽ đồ thị hàm số
| x | -2 | -1 | 0 | 1 | 2 |
| y = 0,5 x 2 | 2 | 0,5 | 0 | 0,5 | 2 |
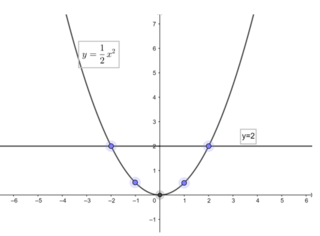
Dựa vào đồ thị ta thấy:
Khi x ≤ 0 thì y ≥ 0

0,5 x y + 1,4 x y = 106,78
1,9 x y = 106,78
y = 106,78 : 1,9
y = 56,2

\(y:0,5+y\times0,5=0,75\)
\(y:\frac{5}{10}+y\times0,5=0,75\)
\(y\times\frac{10}{5}+y\times0,5=0,75\)
\(y\times2+y\times0,5=0,75\)
\(y\times\left(2+05\right)=0,75\)
\(y\times2,5=0,75\)
\(y=0,75:2,5\)
\(y=0,3\)
vậy \(y=0,3\)
ai choi blox fruit ten tui ne kb eeGlv16 mk anhlinhflo

a)(3/2-0,5)/x=7/2+1/4
(3/2-1/2)/x=14/4+1/4
1/x=15/4
x=1:15/4
x=4/15
b)(x*0,25+2010)*2011=(53+2010)*(2012-1)
(x*0,25+2010)*2011=2063*2011
=>0,25x+2010=2063
0,25x=2063-2010
0,25x=53
x=53/0,25
x=212
+ \(\left\{{}\begin{matrix}\left(x-0,5\right)^{2010}\ge0\forall x\\\left|x+y+0,5\right|\ge0\forall x,y\end{matrix}\right.\)
\(\Rightarrow\left(x-0,5\right)^{2010}+\left|x+y+0,5\right|\ge0\forall x,y\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}\left(x-0,5\right)^{2010}=0\\\left|x+y+0,5\right|=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0,5\\y=-1\end{matrix}\right.\)
cảm ơn