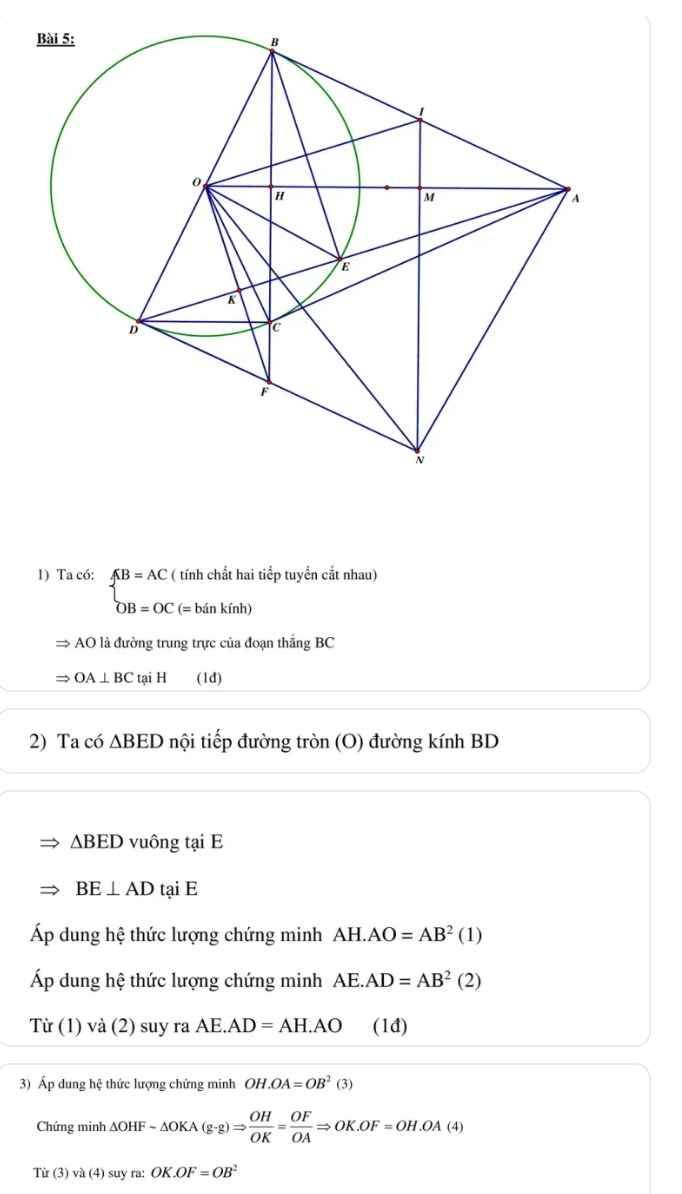
cho (O) và điểm A nằm ngoài (O). Từ A kẻ 2 tiếp tuyến với đường tròn O ( B và C là 2 tiếp điểm). Đường thẳng CO cắt (O) tại điểm thứ 2 là D; đường thẳng AD cắt (O) tại điểm thứ 2 là E; đường thẳng BE cắt AO tại F; H là giao của AO và BC.
a, CM: AE.AD=AH.AO=\(AB^2\) và CM: tứ giác ODEH nội tiếp đường tròn
b,CM: HE vuông góc BF
c, CM: \(\frac{HC^2}{AF^2-EF^2}-\frac{DE}{AE}=1\)