Cho tam giác ABC Cho tam giác ABC. Môt đường thẳng song song với BC cắt AB, AC lần lượt tại D và E sao cho CD^2=AC.AE và AC^2=AB.AD
Giup mình với. Mình cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
+ ΔABC có Aˆ+ABCˆ+ACBˆ=180o. hay 60o+ABCˆ+ACBˆ=180o→ABCˆ+ACBˆ=120o
→ABCˆ+ACBˆ2=60o=ABCˆ2+ACBˆ2=B1ˆ+C1ˆ
+ Gọi CN∩BM=G
+ Δ có B1ˆ+C1ˆ+BGCˆ=180o. Hay 60o+BGCˆ=180o→BGCˆ=120o
+ Gọi GD là tia phân giác BGCˆ→G2ˆ=G3ˆ=60o
+ Tính G1ˆ=G4ˆ=G2ˆ=G3ˆ=60o
+ CM ΔNGB=ΔDGB (gcg) →BN=DB (2 cạnh tương ứng)
+CM ΔMGC=ΔDGC(gcg) →CM=CD (2 cạnh tương ứng)
+ Ta có BC=BD+CD=BN+CM (đpcm)

Qua D kẻ đường thẳng song song với AC và nó cắt cạnh AB ở F.
Ta có: DM//AB hay DM//AF. Mà DF//AC hay DF//AM => DM=AF và DF=AM (T/c đoạn chắn)
DF//AC => ^FDB=^NCE (Đồng vị); BF//EN =>^FBD=^NEC (Đồng vị)
Xét tam giác BFD và tam giác ENC có:
^FDB=^NCE
DB=EC => Tam giác BFD=Tam giác ENC (g.c.g)
^FBD=^NEC
=> DF=CN (2 cạnh tương ứng) . Mà DF=AM (cmt) => AM=CN (đpcm)

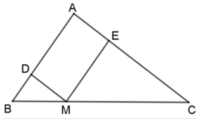
Ta có: MD // AC nên ΔDBM ~ ΔABC. Suy ra :
D B A B = B M B C = D M A C = D B + B M + D M A B + B C + C A
Do đó 1 3 = P B D M P A B C
Chu vi ΔDBM bằng 30. 1 3 = 10cm
Ta có ME // AB nên ΔEMC ~ ΔABC. Suy ra
E M A B = M C B C = E C A C = E M + M C + E C A B + B C + A C
do đó 2 3 = P E M C P A B C
Chu vi ΔEMC bằng 30. 2 3 = 20 cm
Vậy chu vi ΔDBM và chu vi ΔEMC lần lượt là 10cm; 20cm
Đáp án: D

+ Xét \(\Delta ABC\)có :
\(DE//BC\left(gt\right)\)
\(\Rightarrow\frac{AD}{DB}=\frac{AE}{EC}\)( định lí Ta - lét ) (1)
+ Xét \(\Delta DBC\)có :
\(AK//BC\left(gt\right)\)
\(\Rightarrow\frac{AK}{BC}=\frac{AD}{DB}\)( định lí Ta - lét ) (2)
+ Xét \(\Delta BEC\)có:
\(AG//BC\left(gt\right)\)
\(\Rightarrow\frac{AG}{BC}=\frac{AE}{EC}\)( định lí Ta - lét ) (3)
Từ (1) , (2) và (3) \(\Rightarrow\frac{AK}{BC}=\frac{AG}{BC}\)
\(\Rightarrow AK=AG\)
\(\Rightarrow A\)là trung điểm của KG (đpcm)
Chúc bạn học tốt !!!
hay quá thế là đỡ cho mình
Tam giác ABC có DE//BC=>\(\frac{AB}{AD}=\frac{AC}{AE}=>\frac{AE}{AD}=\frac{AC}{AB}\left(1\right)\)
TA có AC^2=AB.AD=>\(\frac{AC}{AB}=\frac{AD}{AC}\)mà (1)=>\(\frac{AD}{AC}=\frac{AE}{AD}\)=> AC.AE=AD^2
Mặt khác CD^2=AC.AE
=>AD=CD