Cho \(\Delta ABC\) với G là trọng tâm. Một đường thẳng bất kì qua G cắt các cạnh AB, AC lần lượt tại M, N. Tính \(\dfrac{AB}{AM}+\dfrac{AC}{AN}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
13 tháng 3 2020
Gọi I,J,K lần lượt là trung điểm của các cạnh BC,CA,AB; các đường thẳng d1,d2 đi qua G và song song với AB,AC và cắt AC,AB tại L,H. Khi đó ta có: GL//AB=>AB/GL=BJ/GJ=3; GL//AM=>GL/AM=NG/MN. Nhân hai đẳng thức theo vế thì được AB/AM=3NG/MN (*). Một cách tương tự ta cũng chứng minh được AC/AN=3MG/MN (*). Cộng (*) và (**) theo vế thì được AB/AM+AC/AN=3(NG+MG)/MN=3.
NN
1
6 tháng 1 2016
hình tự vẽ nha bn! gọi K,I,P lần lượt là tđ của AB,AC,BC
ta có AG/AP=2/3=> S AMG/ABP=2/3=> AM/AB=2/3
ta có AM/AB=2/3,AG/AP=2/3=> MG//BP (định lý talet đảo)
khi MG//BP=> AB/AM=AP/AG (1)
khi GN//PC (MG//BP) => AP/AG=AC/AN (2)
từ (1),(2)=> AB/AM+AC/AN=2AP/AG=2.3/2=3
H9
HT.Phong (9A5)
CTVHS
16 tháng 1
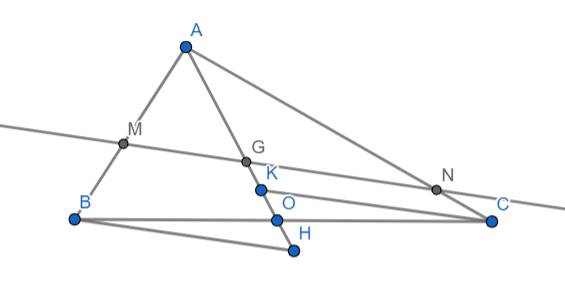
Xét 2 tam giác AMG và ABH ta có:
\(\widehat{BAH}\) chung
\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG)
\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1)
Xét 2 tam giác ANG và ACK có:
\(\widehat{CAK}\) chung
\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN)
\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2)
Xét hai tam giác BOH và COK ta có:
\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh)
\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC)
\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK)
\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\)
\(\Rightarrow HO=OK\) (hai cạnh t.ứng)
\(\Rightarrow HK=2HO\)
Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\)
\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\)
Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)
Gọi D là trung điểm BC, lần lượt kẻ BP và CQ song song MN
\(\Rightarrow AG=\frac{2}{3}AD\)
\(\left\{{}\begin{matrix}\widehat{QCD}=\widehat{PBD}\left(slt\right)\\BD=DC\left(gt\right)\\\widehat{CDQ}=\widehat{PDQ}\left(dd\right)\end{matrix}\right.\) \(\Rightarrow\Delta CDQ=\Delta BDP\Rightarrow DQ=DP\)
\(MG//BP\Rightarrow\frac{AB}{AM}=\frac{AP}{AG}=\frac{AD+DP}{AG}\)
\(GN//CQ\Rightarrow\frac{AC}{AN}=\frac{AQ}{AG}=\frac{AD-DQ}{AG}\)
\(\Rightarrow\frac{AB}{AM}+\frac{AC}{AN}=\frac{AD+DP+AD-DQ}{AG}=\frac{2AD}{AG}=\frac{2AD}{\frac{2}{3}AD}=3\)