Cho tam giác ABC, phân giác \(\widehat{B}\)cắt phân giác góc\(\widehat{C}\)tại O
a)CMR: \(\widehat{BOC}\)tù, từ đó tìm cạnh lớn nhất trong tam giác BOC
b) Gỉa sử OB<OC. So sánh AB và AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

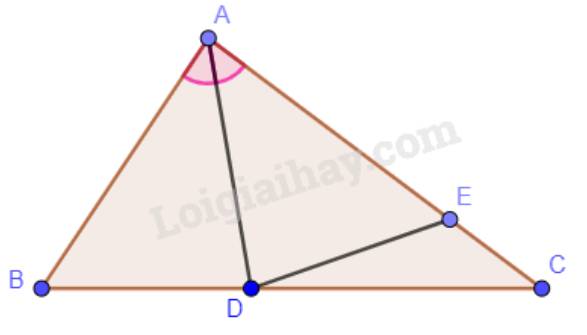
a) Ta có: \(\widehat {BAD} = \widehat {CAD}\)(vì AD là phân giác của góc BAC).
Mà \(\widehat B > \widehat C\)nên \(\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ - (\widehat B + \widehat {BAD}) < 180^\circ - (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}\)
b) Xét hai tam giác ADB và tam giác ADE có:
\(\widehat {ADB} = \widehat {ADE}\);
AD chung;
\(\widehat {BAD} = \widehat {EAD}\).
Vậy \(\Delta ABD = \Delta AED\) (g.c.g)
Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
Trong tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).

a) Tam giác ABD và CBD có:
AB=CB (do tam giác ABC đều)
góc ABD = góc CBD (vì BD là tia phân giác của góc ABC)
BD chung
=> tam giác ABD=tam giác CBD (c.g.c) => góc BDA=góc BDC (2 góc tương ứng)
mà 2 góc này kề bù suy ra góc BDA=góc BDC=90o => BD vuông góc với AC
Chứng minh tương tự được CE vuông góc với AB
b) Tam giác ABC đều nên góc BAC=góc ABC=góc ACB=60o
mà: góc ABD=góc CBD (vì BD là tia phân giác góc ABC); góc ACE=góc BCE (vì CE là tia phân giác góc ACB)
=> góc ABD=góc CBD=góc ACE=góc BCE
Tam giác BOC có: góc CBD=góc BCE => tam giác BOC cân tại O => OB=OC(1)
Tam giác BAO và tam giác CAO có: AB=CA(\(\Delta ABC\)cân tại A);cạnh AO chung;OB=OC(cmt)
=>Tam giác BAO = tam giác CAO (c.c.c) => góc BAO=góc CAO (2 góc tương ứng)
mà góc ABC=BAC nên góc ABD=góc CBD=góc BAO=góc CAO=> tam giác BAO cân tại O=>OA=OB(2)
Từ (1) và (2) => OA=OB=OC
c) phần này dễ nên tự làm nhé

Xin chào đồng loại. À k, fải là xin chào "c - hó" ms đúng tên của pạn chứ nhỉ, bạn "depgiaicogisaidau" thân yêu!
P/s: mai đổi thành "lachocogisaidau" nha!

a/ Vì \(\widehat{B}=\widehat{C}\)(gt)
mà BD, CE là tia p.g của \(\widehat{B},\widehat{C}\)
\(\Rightarrow\widehat{ABD}=\widehat{DBC}=\widehat{ACE}=\widehat{ECB}\)
Xét tam giác BCD và tam giác CBE ta có:
\(\hept{\begin{cases}\widehat{B}=\widehat{C}\\BC:canh\\\widehat{DBC}=\widehat{ECB}\left(gt\right)\end{cases}}chung\)
suy ra tam giác BCD bằng tam giác CBE ( c.g.c )
Nhớ k cho mình nhé! Thank you!!!
b/ Vì \(\widehat{OBC}=\widehat{OCB}\left(cmt\right)\)
suy ra tam giác OBC cân tại O
suy ra OB = OC
Nhớ k cho mình nhé! Thank you!!!