Chp \(\left(P\right)\) \(y=\frac{x^2}{4}\)
a. Vẽ đồ thị hàm số \(\left(P\right)\)
b. Tìm tọa độ giao điểm với đường thẳng \(3x-4y-24=0\)
c. Lập phương trình tiếp tuyến của \(\left(P\right)\) tại \(A\left(8;0\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Bạn bổ sung đề bài đi bạn
2: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{4}{2m-1}\\y=0\end{matrix}\right.\)
=>\(OA=\sqrt{\left(\dfrac{4}{2m-1}-0\right)^2+\left(0-0\right)^2}=\dfrac{4}{\left|2m-1\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)\cdot0-4=-4\end{matrix}\right.\)
=>OB=4
Để ΔOAB cân tại O thì OA=OB
=>\(\dfrac{4}{\left|2m-1\right|}=4\)
=>\(\dfrac{1}{\left|2m-1\right|}=1\)
=>\(\left|2m-1\right|=1\)
=>\(\left[{}\begin{matrix}2m-1=1\\2m-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m=2\\2m=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)

có:
+) đạo hàm của f(x) = f'(x) = 3x2
+) phương trình tiếp tuyến là : y= f'(x).(x-x0) + f(x0)
=> y = 3x2.(x-1) + 13 + 3 = 3x3 - 3x2 + 4

Ta có \(y'=3x^2-6x\)
Gọi \(M\left(x_0;x_0^3-3x^3_0+4\right)\) là điểm thuộc đồ thị (C)
Hệ số góc tiếp tuyến của đồ thị (C) tại M là \(k=y'\left(x_0\right)=3x_0^2-6x_0\)
Vì tiếp tuyến của đồ thị tại M song song với đường thẳng \(d:y=9x+3\) nên có hệ số góc \(k=9\)
\(\Leftrightarrow3x_0^2-6x_0=9\Leftrightarrow x_0^2-2x_0-3=0\Leftrightarrow x_0=-1\) V \(x_0=3\)
Vậy \(M\left(-1;0\right)\) và \(M\left(3;4\right)\) đều không thuộc d nên thỏa mãn yêu cầu bài toán

a)
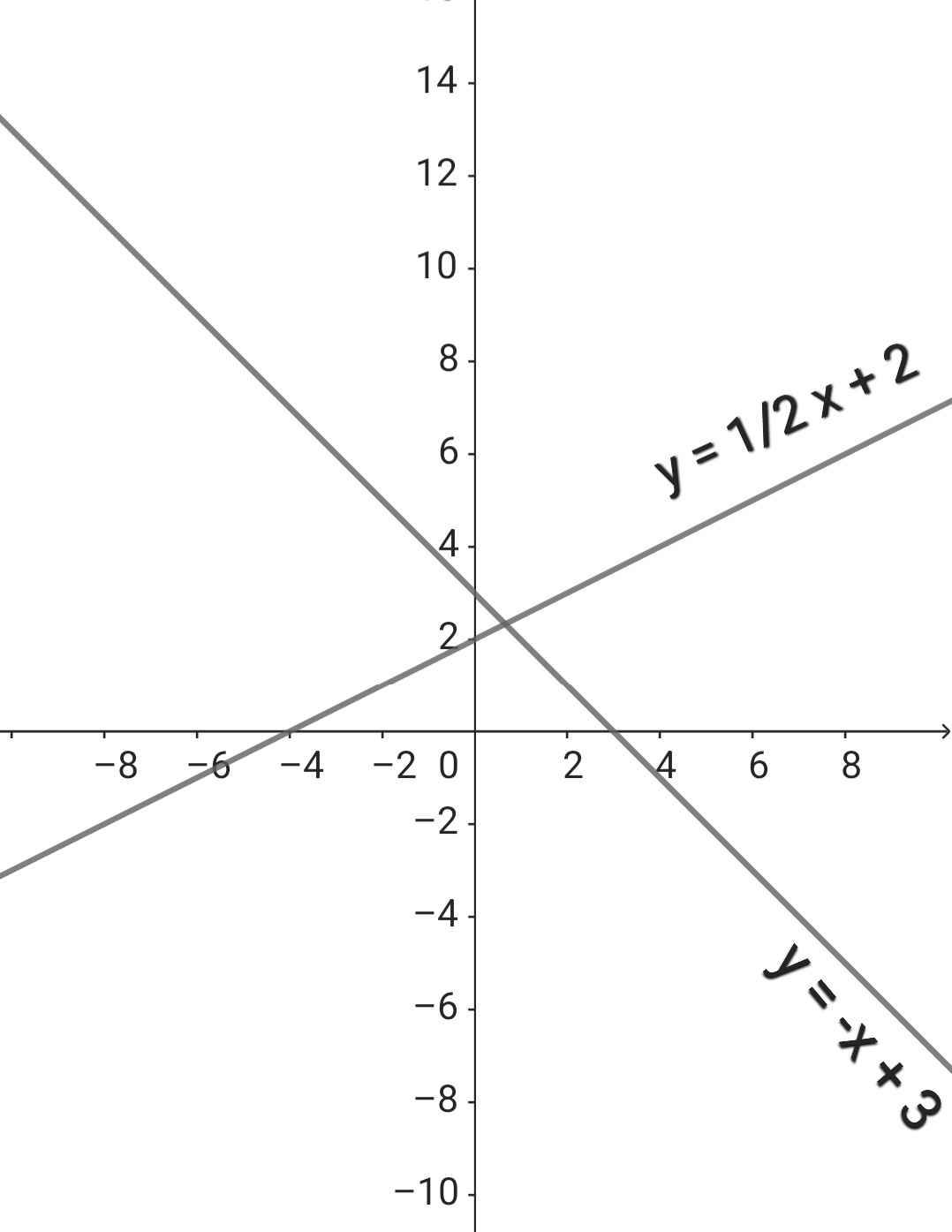 b) Phương trình hoành độ giao điểm của (D₁) và (D₂):
b) Phương trình hoành độ giao điểm của (D₁) và (D₂):
x/2 + 2 = -x + 3
⇔ x/2 + x = 3 - 2
⇔ 3x/2 = 1
⇔ x = 1 : 3/2
⇔ x = 2/3
⇒ y = -2/3 + 3
⇔ y = 7/3
Vậy A(2/3; 7/3)
c) Do (D) // (D₂)
⇒ a = -1
⇒ (D): y = -x + b
Thay x = -2 vào (D₁) ta có:
y = 1/2 . (-2) + 2
⇔ y = 1
Thay x = -2; y = 1 vào (D) ta có:
2 + b = 1
⇔ b = 1 - 2
⇔ b = -1
Vậy (D): y = -x - 1
Bài 3:
a)
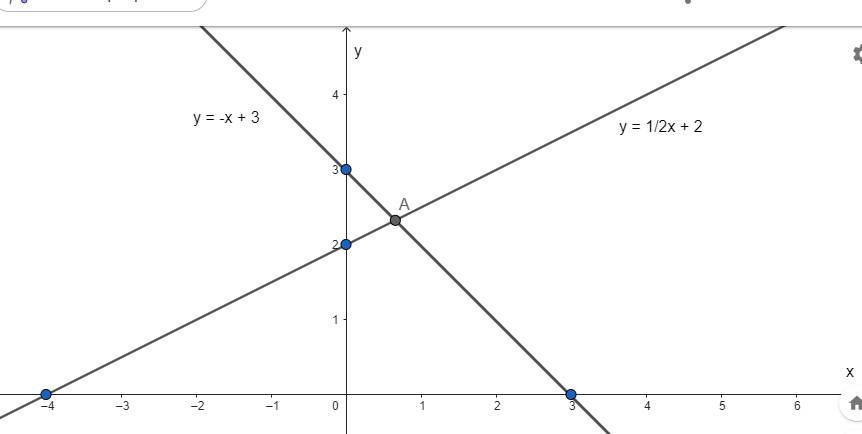
b) Xét phương trình hoành độ giao điểm của D1 và D2 có: y = y
⇒ \(\dfrac{1}{2}x+2=-x+3\)
⇒ \(\dfrac{3}{2}x=1\)
⇒ \(x=\dfrac{2}{3}\)
Thay \(x=\dfrac{2}{3}\) vào D2 có \(y=-\dfrac{2}{3}+3=\dfrac{7}{3}\)
⇒ \(A\left(\dfrac{2}{3};\dfrac{7}{3}\right)\)
Vậy D1 cắt D2 tại \(A\left(\dfrac{2}{3};\dfrac{7}{3}\right)\)
c) ĐK: a ≠ 0
Vì (D) // (D2)
⇒ \(\left\{{}\begin{matrix}a=-1\left(TM\right)\\b\ne3\end{matrix}\right.\)
Vì (D) cắt (D1) tại điểm có hoành độ x = 2
Tức là x = -2 và y = 1
Thay x = 2; y = 0 và a = -1(TMĐK) vào D có:
⇒ \(-2\cdot-1+b=1\)
⇒ \(b+2=1\)
⇒ \(b=-1\left(TM\right)\)
Vậy (D) : y = \(-x-1\)

Với m = 1, ta có \(\left(C_1\right):y=\frac{x+1}{x-1}\)
a. Gọi d là đường thẳng đi qua P, có hệ số góc k => \(d:y=k\left(x-3\right)+1\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=k\left(x-3\right)+1\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(\frac{x+1}{x-1}=\frac{-2}{\left(x-1\right)^2}\left(x-3\right)+1\Leftrightarrow x=2\)
\(\Rightarrow k=-2\Rightarrow\) phương trình tiếp tuyến : \(y=-2x+7\)
b. Gọi d là đường thẳng đi qua A, có hệ số góc k : \(d:y=k\left(x-2\right)-1\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=k\left(x-2\right)-1\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(\frac{x+1}{x-1}=\frac{-2}{\left(x-1\right)^2}\left(x-2\right)-1\Leftrightarrow x=\pm\sqrt{2}\)
* \(x=\sqrt{2}\Rightarrow k=-2\left(3+2\sqrt{2}\right)\Rightarrow\) phương trình tiếp tuyến : \(y=-2\left(3+2\sqrt{2}\right)x+11+8\sqrt{2}\)
* \(x=-\sqrt{2}\Rightarrow k=-2\left(3-2\sqrt{2}\right)\Rightarrow\) phương trình tiếp tuyến : \(y=-2\left(3-2\sqrt{2}\right)x+11-8\sqrt{2}\)
c. Ta có : \(y'=\frac{m^2-2m-1}{\left(x+m-2\right)^2}\)Tiếp tuyến tại điểm có hoành độ x = 1 vuông góc với đường thẳng\(y=x+1\Leftrightarrow y'\left(1\right)=-1\Leftrightarrow\frac{m^2-2m-1}{\left(m-1\right)^2}=-1\)\(\Leftrightarrow m=0;m=2\)

a. Tiếp tuyến của \(\left(C_m\right)\) tại điểm có hoành độ x = 1 có phương trình :
\(y=\left(m-2\right)\left(x-1\right)+3m-2=\left(m-2\right)x+3m\)
Yêu cầu của bài toán khi và chỉ khi \(\begin{cases}m-2=3\\2m\ne10\end{cases}\) vô nghiệm
Vậy không tồn tại m thỏa mãn yêu cầu bài toán
b. Ta có \(y'=3\left(x^2-\frac{4}{3}x+\frac{4}{9}\right)+m-\frac{7}{3}=3\left(x-\frac{2}{3}\right)^2+m-\frac{7}{3}\)
Suy ra \(y'\ge m-\frac{7}{3}\)
Tiếp tuyến tại điểm có hoành độ \(x=\frac{2}{3}\) có hệ số góc nhỏ nhất và hệ số góc có giá trị \(k=m-\frac{7}{3}\)
Yêu cầu bài toán \(\Leftrightarrow k.2=-1\Leftrightarrow\left(m-\frac{7}{3}\right).2=-1\Leftrightarrow m=\frac{11}{6}\)

\(y'=8x^3-8x\)
a. Đường thẳng \(x-48y+1=0\) có hệ số góc \(\dfrac{1}{48}\) nên tiếp tuyến có hệ số góc \(k=-48\)
\(\Rightarrow8x^3-8x=-48\Rightarrow x^3-x+6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+3\right)=0\Rightarrow x=-2\)
\(y'\left(-2\right)=47\)
Phương trình tiếp tuyến: \(y=-48\left(x+2\right)+47\)
b. Gọi tiếp điểm có hoành độ \(x_0\)
Phương trình tiếp tuyến: \(y=\left(8x_0^3-8x_0\right)\left(x-x_0\right)+2x^4_0-4x^2_0-1\) (1)
Do tiếp tuyến qua A:
\(\Rightarrow-3=\left(8x_0^3-8x_0\right)\left(1-x_0\right)+2x_0^4-4x^2_0-1\)
\(\Leftrightarrow3x_0^4-4x_0^3-2x_0^2+4x_0-1=0\)
\(\Leftrightarrow\left(x_0-1\right)^2\left(3x_0^2+2x_0-1\right)=0\Rightarrow\left[{}\begin{matrix}x_0=1\\x_0=-1\\x_0=\dfrac{1}{3}\end{matrix}\right.\)
Có 3 tiếp tuyến thỏa mãn. Thay lần lượt các giá trị \(x_0\) bên trên vào (1) là được
a, Bảng giá trị tương ứng x và y
b, Viết lại cho đẹp \(3x-4y-24=0\Rightarrow\left(d\right)y=\frac{3}{4}x-6\)
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình
\(\frac{x^2}{4}=\frac{3}{4}x-6\)
\(\Leftrightarrow x^2=3x-24\)
\(\Leftrightarrow x^2-3x+24=0\)
\(\Leftrightarrow\left(x-\frac{3}{2}\right)^2+\frac{87}{4}=0\)
Pt vô nghiệm nên (d) không cắt (P)
c, Gọi tiếp tuyến của (P) đi qua điểm A(8;0) là (d') y = ax + b
Hoành độ giao điểm (d') và (P) là nghiệm của pt
\(\frac{x^2}{4}=ax+b\)
\(\Leftrightarrow x^2-4ax-4b=0\)
Để (d') tiếp xúc (P) thì \(\Delta'=0\)
\(\Leftrightarrow4a^2+4b=0\)
\(\Leftrightarrow a^2+b=0\)
Vì \(A\in\left(d'\right)\Rightarrow0=8a+b\)
Ta có hệ \(\hept{\begin{cases}a^2+b=0\\8a+b=0\end{cases}}\)
\(\Rightarrow a^2-8a=0\)
\(\Rightarrow\orbr{\begin{cases}a=0\Rightarrow b=0\\a=8\Rightarrow b=-64\end{cases}}\)
*Với a = 0 ; b = 0 thì (d') y = 0 => (d') là trục Ox
*Với a = 8 ; b = -64 thì (d') y = 8x - 64
Vậy tiếp tuyến của (P) tại A(8;0) là trục Ox hoặc đường thằng y = 8x - 64