1 cho cho tam giác ABC, điểm I nằm trong tam giác đó biết <AIB +<ACI =90độ -<A/2 và BI là tia phân giác của góc B. c/m CI là phân giác của <C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 12 2015
132; 123; 231; 213; 312; 321; 510; 420; 240; 150
Tick mình!
22 tháng 2 2020
Câu hỏi của Nguyễn Vũ Thu Hương - Toán lớp 7 - Học toán với OnlineMath
CM
25 tháng 1 2017
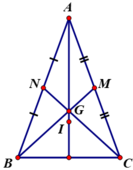
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà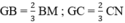 
(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
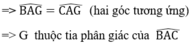
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của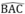 
Vì G, I cùng thuộc tia phân giác của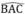 
nên A, G, I thẳng hàng
19 tháng 4 2017
Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = BM; GC = CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> => G thuộc phân giác của
Mà ∆ABI = ∆ACI (c.c.c)
=> => I thuộc phân giác của
Vì G, I cùng thuộc phân giác của nên A, G, I thẳng hàng
19 tháng 4 2017
Hướng dẫn:
a) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
ˆBAD=ˆCADBAD^=CAD^
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=> ˆDBC=ˆDCB
16 tháng 5 2016
Gọi M,N,P lần lượt là trung điểm các cạnh AB,AC,BC
Do đó diện tích AMN = diện tích BMP = diện tích ANP = \(\frac{1}{4}\) diện tích ABC
Theo nguyên lý di - rich - le thì trong 9 điểm đề bài cho,ít nhất có 3 điểm nằm trong tam giác AMN,BMP hoặc tam giác ANP
Gọi 3 điểm đó là H,I,K
Chẳng hạn 3 điểm H,I,K nằm trong tam giác ANP
= > diện tích HIK < diện tích ANP = \(\frac{1}{4}\) diện tích tam giác ABC
Vậy sẽ có một tam giác nhỏ hơn \(\frac{1}{4}\) diện tích tam giác ABC
Đáp số : Sẽ có một tam giác nhỏ hơn \(\frac{1}{4}\) diện tích tam giác ABC
19 tháng 9 2019
Gọi giao điểm của BG với AC là M ;
CG với AB là N
Vì G là trọng tâm của \(\Delta ABC\)
nên BM, CN, là trung tuyến
Mặt khác \(\Delta ABC\) cân tại A
Nên BM = CN
Ta có : \(GB=\frac{1}{2}BM;GC=\frac{2}{3}CN\) (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó : \(\Delta AGB=\Delta AGC\left(c.c.c\right)\)
\(\Rightarrow\widehat{BAG}=\widehat{CAG}\Rightarrow G\) thuộc phân giác của \(\widehat{BAC}\)
Mà \(\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\Rightarrow\widehat{BAI}=\widehat{CAI}\Rightarrow I\) thuộc phân giác của \(\widehat{BAC}\)
Vì G, I cùng thuộc phân giác của \(\widehat{BAC}\) nên A, G, I thẳng hàng
Chúc bạn học tốt !!!
KN
17 tháng 2 2019
Giải
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà \(GB=\frac{2}{3}BM;GC=\frac{2}{3}CN\)(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
\(\Rightarrow\widehat{BAG}=\widehat{CAG}\)( hai góc tương ứng )
\(\Rightarrow\)G là trọng tâm của \(\widehat{BAC}\)
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của \(\widehat{BAC}\)
Vì G, I cùng thuộc tia phân giác của \(\widehat{BAC}\)nên A, G, I thẳng hàng
10 tháng 4 2016
Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = BM; GC = CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> => G thuộc phân giác của
Mà ∆ABI = ∆ACI (c.c.c)
=> => I thuộc phân giác của
Vì G, I cùng thuộc phân giác của nên A, G, I thẳng hàng
2 tháng 4 2018
Vì G là trọng tâm của tam giác ABC trên D thuộc đường trung tuyến AM (1)
Vì I là giao điểm các phân giác của tam giác ABC nên AI là tia phân giác của góc A mà trong tam giác cân phân giác của góc ở đỉnh của tam giác cũng là trung tuyến do đó I thuộc trực tuyến AM(2)
Từ (1) và (2 )suy ra 3 điểm A,I,G thẳng hàng