Cho tam giác MNP có góc N = 1000 và M-P = 200. Tính góc M và góc P.
GIÚP LẸ CẢM ƠN TRƯỚC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(PQ = n.\cos a,PQ = m.\cos b\)
b) \(MQ = n.\sin a,PN = m.\sin b \Rightarrow MN = n.\sin a + m.\sin b\)
\(\begin{array}{l}{S_{MPQ}} = \frac{1}{2}m.\cos b.n.\sin a = \frac{1}{2}m.n.\cos b.\sin a\\{S_{NPQ}} = \frac{1}{2}n.\cos a.m.\sin b = \frac{1}{2}m.n.\cos a.\sin b\\{S_{MNP}} = \frac{1}{2}m.n.\sin \left( {a + b} \right)\end{array}\)
c) \({S_{MNP}} = {S_{MPQ}} + {S_{NPQ}} \Rightarrow \frac{1}{2}m.n.\cos b.\sin a + \frac{1}{2}m.n.\cos a.\sin b = \frac{1}{2}m.n.\sin \left( {a + b} \right)\)
\( \Rightarrow \sin \left( {a + b} \right) = \sin a.\cos b + \cos a.\sin b\)
d) \(\sin \left( {a - b} \right) = \sin \left[ {a + \left( { - b} \right)} \right] = \sin a.\cos \left( { - b} \right) + \cos a.\sin \left( { - b} \right) = \sin a.\cos b - \cos a.\sin b\)

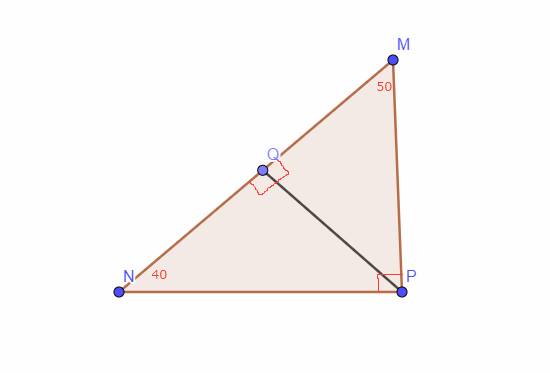
Xét Tam giác `MPQ` có:
\(\widehat{M}+\widehat{MPQ}+\widehat{MQP}=180^0\) (đli tổng 2 góc trong 1 Tam giác)
\(50^0+\widehat{MPQ}+90^0=180^0\)
`=>` \(\widehat{MPQ}=40^0\)
\(\widehat{MQP}+\widehat{NQP}=180^0\) (kề bù)
\(90^0+\widehat{NQP}=180^0\)
`=>` \(\widehat{NQP}=90^0\)
Xét Tam giác `NPQ` có:
\(\widehat{N}+\widehat{NQP}+\widehat{NPQ}=180^0\)
\(40^0+90^0+\widehat{NPQ}=180^0\)
`=>` \(\widehat{NPQ}=50^0\)

a: Xét ΔMNP có MN=MP
nên ΔMNP cân tại M
hay \(\widehat{N}=\widehat{P}\)

Theo bài ra ta có: M=2x; N=3x; P=5x
Xét tam giác MNP có
M+N+P=180* (tổng 3 góc của tam giác)
<=> 2x+3x+5x=180*
<=>x(2+3+5)=180*
=> 10x=180* => x=18*
=> M=2x=2.18*=36*
=> N=3x=3.18*=54*
=> P=5x=5.18*=90*
Theo bài ra ta có: M=2x; N=3x; P=5x
Xét tam giác MNP có
M+N+P=180* (tổng 3 góc của tam giác)
<=> 2x+3x+5x=180*
<=>x(2+3+5)=180*
=> 10x=180* => x=18*
=> M=2x=2.18*=36*
=> N=3x=3.18*=54*
=> P=5x=5.18*=90
chúc bn hok tốt NHa@_@
Tổng số đo góc của 2 góc M và P là: 180-100=80 độ
Góc P=(80-20):2=30 độ
Góc M=30+20=50 độ
HT
Xét tam giác MNP có:
\(\widehat{M}+\widehat{P}+\widehat{N}=180^0\)(tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{M}+\widehat{P}=180^0-\widehat{N}=180^0-100^0=80^0\)
Ta có: \(\left\{{}\begin{matrix}\widehat{M}+\widehat{P}=80^0\\\widehat{M}-\widehat{P}=20^0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\widehat{M}=\left(80^0+20^0\right):2=50^0\\\widehat{N}=\left(80^0-20^0\right):2=30^0\end{matrix}\right.\)