Cho tam giác abc có ab=16,ac=14,b=60 độ.tính bc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
1
23 tháng 7 2017
trong tam giac vuong ABH ta co \(AH=\sin B\cdot AB\) \(\Rightarrow AH=8\sqrt{3}\)
\(BH=\cos B\cdot AB=8\)
trong tam giac AHC co \(HC^2+AH^2=AC^2\Rightarrow HC^2=14^2-\left(8\sqrt{3}\right)^2=4\Rightarrow HC=2\)
\(\Rightarrow BC=BH+HC=8+2=10\)
\(\Rightarrow SABC=\frac{1}{2}BC\cdot AH=\frac{1}{2}\cdot10\cdot8\sqrt{3}=40\sqrt{3}\)
NM
0
IT
1
14 tháng 7 2016
Ta có: AC2 = AB2 + BC2 - 2AB.BC.cos(ABC)
<=> 142 = 162 + BC2 -2.16.BC.cos(60)
<=> BC2 - 16BC + 60 = 0
<=> BC = 6 hoặc BC = 10
Thoe bất đẳng thức tam giác thì car2 trường hợp trên đều thỏa mãn
Vậy BC = 6 hoặc BC = 10
9 tháng 11 2023
\(\left[{}\begin{matrix}\\\\\\\end{matrix}\right.\prod\limits^{ }_{ }\int_{ }^{ }dx\sinh_{ }^{ }⋮\begin{matrix}&&&\\&&&\\&&&\\&&&\\&&&\\&&&\end{matrix}\right.\Cap\begin{matrix}&&\\&&\\&&\\&&\\&&\\&&\end{matrix}\right.\)
KP
1
CM
3 tháng 3 2017
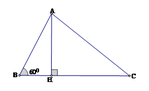
Kẻ đường cao AH
Xét tam giác vuông ABH, ta có:
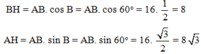
Áp dụng định lý Py-ta-go vào tam giác vuông AHC ta có:
Suy ra HC = 2.
Vậy BC = CH + HB = 2 + 8 = 10
Đáp án cần chọn là: A
VC
1
DT
11 tháng 7 2016
Tam giác ABC vuông tại A:
\(tanB=\frac{AC}{AB}\Rightarrow AC=\tan B.AB=\tan40^o.17\approx14,265cm\)
\(\cos B=\frac{AB}{BC}\Rightarrow BC=\frac{AB}{\cos B}=\frac{17}{cos40^o}\approx22,192cm\)
\(\cos C=\frac{AC}{BC}=\frac{14,265}{22,192}\approx0,643\Rightarrow C\approx50^o\)
kẻ AH vuông góc với BC
Ta có HB=1/2AB SUY RA HB=8cm
do đó bc=10cm