\(\text{(X+√3)/(√X+√(X+√3) )+(X-√3)/(√X-√(X-√3) )=√X}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 7 2023
a: TH1: x<-1/2
PT sẽ là -2x-1+3-x=4
=>-3x+2=4
=>-3x=2
=>x=-2/3(nhận)
TH2: -1/2<=x<3
Pt sẽ là 2x+1+3-x=4
=>x+4=4
=>x=0(nhận)
TH3: x>=3
=>x-3+2x+1=4
=>3x-2=4
=>x=2(loại)
b: TH1: x<-3/2
Pt sẽ là -2x-3+3-4x=x
=>-6x=x
=>x=0(loại)
TH2: -3/2<=x<3/4
PT sẽ là 2x+3+3-4x=x
=>-2x+6-x=0
=>-3x=-6
=>x=2(loại)
TH3: x>=3/4
PT sẽ là 2x+3+4x-3=x
=>6x=x
=>x=0(loại)
18 tháng 12 2021
c: \(E=\dfrac{\left(x-5\right)^2}{x\left(x-5\right)}=\dfrac{x-5}{x}\)
10 tháng 3 2020
\(\frac{5.2^{18}.3^{18}.2^{12}-2.2^{28}.3^{14}.3^4}{5.2^{28}.3^{18}-7.2^{29}.3^{18}}=\frac{5.2^{30}.3^{18}-2^{29}.3^{18}}{5.2^{28}.3^{18}-7.2^{29}.3^{18}}=\frac{2^{29}.3^{18}\left(5.2-1\right)}{2^{28}.3^{18}\left(5-7.2\right)}\)
\(\frac{2^{29}.3^{18}.9}{2^{28}.3^{18}.-9}=\frac{2.9}{-9}=-2\)
XO
27 tháng 9 2023
ĐKXĐ \(3x^2-5x+1\ge0;x^2-2\ge0;x^2-x-1\ge0\)
Ta có : \(\sqrt{3x^2-5x+1}-\sqrt{x^2-2}=\sqrt{3.\left(x^2-x-1\right)}-\sqrt{x^2-3x+4}\)
\(\Leftrightarrow\sqrt{3x^2-5x+1}-\sqrt{3\left(x^2-x-1\right)}=\sqrt{x^2-2}-\sqrt{x^2-3x+4}\)
\(\Leftrightarrow\dfrac{3x^2-5x+1-3.\left(x^2-x-1\right)}{\sqrt{3x^2-5x+1}+\sqrt{3\left(x^2-x-1\right)}}=\dfrac{x^2-2-x^2+3x-4}{\sqrt{x^2-2}+\sqrt{x^2-3x+4}}\)
\(\Leftrightarrow\dfrac{-2x+4}{\sqrt{3x^2-5x+1}+\sqrt{3\left(x^2-x-1\right)}}=\dfrac{3x-6}{\sqrt{x^2-2}+\sqrt{x^2-3x+4}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\\dfrac{3}{\sqrt{x^2-2}+\sqrt{x^2-3x+4}}+\dfrac{2}{\sqrt{3x^2-5x+1}+\sqrt{3\left(x^2-x-1\right)}}=0\left(∗\right)\end{matrix}\right.\)
Xét phương trình (*) ta có VT > 0 \(\forall x\) mà VP = 0
nên (*) vô nghiệm
Vậy x = 2 là nghiệm phương trình
8 tháng 3 2022
\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
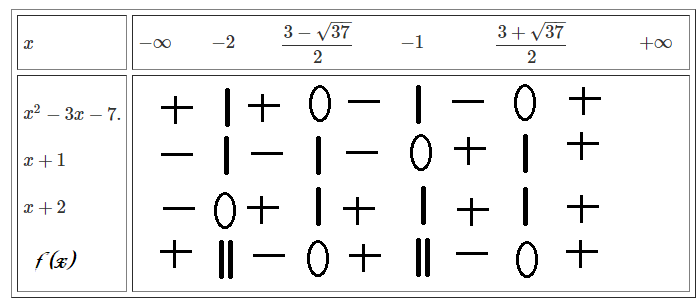
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
22 tháng 10 2021
\(a,\Leftrightarrow2x^3-x^2+ax+b=\left(x-1\right)\left(x+1\right)\cdot a\left(x\right)\)
Thay \(x=1\Leftrightarrow2-1+a+b=0\Leftrightarrow a+b=-1\)
Thay \(x=-1\Leftrightarrow-2-1-a+b=0\Leftrightarrow b-a=3\)
Từ đó ta được \(\left\{{}\begin{matrix}a+b=-1\\-a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=1\end{matrix}\right.\)
\(b,\Leftrightarrow ax^3+bx^2+2x-1=\left(x-1\right)\left(x+6\right)\cdot b\left(x\right)\)
Thay \(x=1\Leftrightarrow a+b+2-1=0\Leftrightarrow a+b=-1\)
Thay \(x=-6\Leftrightarrow-216a+36b+12-1=0\Leftrightarrow216a-36b=11\)
Từ đó ta được \(\left\{{}\begin{matrix}a+b=-1\\216a-36b=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{25}{252}\\b=-\dfrac{227}{252}\end{matrix}\right.\)
\(c,\Leftrightarrow ax^4+bx^3+1=\left(x+1\right)^2\cdot c\left(x\right)\)
Thay \(x=-1\Leftrightarrow a-b+1=0\Leftrightarrow b=a+1\)
\(\Leftrightarrow ax^4+\left(a+1\right)x^3+1⋮\left(x+1\right)\\ \Leftrightarrow ax^4+ax^3+x^3+1⋮\left(x+1\right)\\ \Leftrightarrow ax^3\left(x+1\right)+\left(x+1\right)\left(x^2-x+1\right)⋮\left(x+1\right)\\ \Leftrightarrow\left(x+1\right)\left(ax^3+x^2-x+1\right)⋮\left(x+1\right)\\ \Leftrightarrow ax^3+x^2-x+1⋮\left(x+1\right)\)
Thay \(x=-1\Leftrightarrow-a+1+1+1=0\Leftrightarrow a=3\Leftrightarrow b=4\)
8 tháng 2 2022
ĐKXĐ: \(x\ne\pm3\)
\(P=\left[\dfrac{x\left(x+3\right)}{x^2\left(x+3\right)+9\left(x+3\right)}+\dfrac{3}{x^2+9}\right]:\left[\dfrac{1}{x-3}-\dfrac{6x}{x^2\left(x-3\right)+9\left(x-3\right)}\right]\)
\(=\left[\dfrac{x\left(x+3\right)}{\left(x+3\right)\left(x^2+9\right)}+\dfrac{3}{x^2+9}\right]:\left[\dfrac{1}{x-3}-\dfrac{6x}{\left(x-3\right)\left(x^2+9\right)}\right]\)
\(=\dfrac{x+3}{x^2+9}:\dfrac{x^2+9-6x}{\left(x-3\right)\left(x^2+9\right)}=\dfrac{x+3}{x^2+9}.\dfrac{\left(x-3\right)\left(x^2+9\right)}{\left(x-3\right)^2}=\dfrac{x+3}{x-3}\)
Ý 2 mình k hiểu ý bạn lắm
\(P=\dfrac{x+3}{x-3}=\dfrac{x-3+6}{x-3}=1+\dfrac{6}{x-3}\in Z\)
\(\Leftrightarrow\left(x-3\right)\inƯ\left(6\right)=\left\{-6;-3;-2;-1;1;2;3;6\right\}\)
Kết hợp vs ĐKXĐ \(\Rightarrow x\in\left\{0;1;2;4;5;6;9\right\}\)
4 tháng 9 2023
\(P=\dfrac{x^4+5x^3-20x^2-27x+30}{x^2+4x-21}\left(1\right)\)
Điều kiện xác định khi và chỉ khi
\(x^2+4x-21\ne0\)
\(\Leftrightarrow x^2+7x-3x-21\ne0\)
\(\Leftrightarrow x\left(x+7\right)-3\left(x+7\right)\ne0\)
\(\Leftrightarrow\left(x-3\right)\left(x+7\right)\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne3\\x\ne-7\end{matrix}\right.\)
Theo đề bài : \(\)
\(x=\sqrt[]{31-12\sqrt[]{3}}=\sqrt[]{27-12\sqrt[]{3}+4}=\sqrt[]{\left(3\sqrt[]{3}-2\right)^2}=\left|3\sqrt[]{3}-2\right|=3\sqrt[]{3}-2\)
\(\left(1\right)\Leftrightarrow P=\dfrac{x^4-3x^3+8x^3-24x^2+4x^2-12x-15x+45-15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{x^3\left(x-3\right)+8x^2\left(x-3\right)+4x\left(x-3\right)-15\left(x-3\right)-15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{\left(x-3\right)\left(x^3+8x^2+4x-15\right)-15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{x^3+8x^2+4x-15}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{x^3+7x^2+x^2+7x-3x-15}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{x^2\left(x+7\right)+x\left(x+7\right)-3\left(x+7\right)+6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=\dfrac{\left(x^2+x-3\right)\left(x+7\right)+6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)
\(\Leftrightarrow P=x^2+x-3+\dfrac{6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)
Thay \(x=3\sqrt[]{3}-2\) vào \(P\) ta được
\(\Leftrightarrow P=\left(3\sqrt[]{3}-2\right)^2+3\sqrt[]{3}-2-3+\dfrac{6}{3\sqrt[]{3}-2+7}-\dfrac{15}{\left(3\sqrt[]{3}-2-3\right)\left(3\sqrt[]{3}-2+7\right)}\)
\(\Leftrightarrow P=31-12\sqrt[]{3}+3\sqrt[]{3}-5+\dfrac{6}{3\sqrt[]{3}+5}-\dfrac{15}{\left(3\sqrt[]{3}-5\right)\left(3\sqrt[]{3}+5\right)}\)
\(\Leftrightarrow P=26-9\sqrt[]{3}+\dfrac{6\left(3\sqrt[]{3}-5\right)}{\left(3\sqrt[]{3}+5\right)\left(3\sqrt[]{3}-5\right)}-\dfrac{15}{\left(3\sqrt[]{3}\right)^2-5^2}\)
\(\Leftrightarrow P=26-9\sqrt[]{3}+\dfrac{6\left(3\sqrt[]{3}-5\right)}{2}-\dfrac{15}{2}\)
\(\Leftrightarrow P=\dfrac{37}{2}-9\sqrt[]{3}+3\left(3\sqrt[]{3}-5\right)\)
\(\Leftrightarrow P=\dfrac{37}{2}-9\sqrt[]{3}+9\sqrt[]{3}-15\)
\(\Leftrightarrow P=\dfrac{37}{2}-15=\dfrac{7}{2}\)