1.Cho tam giác ABC có D là trung điểm của BC và AD là phân giác của A, kẻ DE \(\perp\)AB, DF \(\perp\)AC. CMR
a)DE = DF
b)B = C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
29 tháng 8 2019
Tham khảo:
a) HK là đường trung tuyến trong △ADH vuông nên HK=AD2
Tương tự, FK=AD2=HK. Suy ra △KFH cân tại K
Ta có AKF^=180∘−2KAF^ do △AKF cân tại K. Tương tự, HKD^=180∘−2KDH^
Suy raAKF^+HKD^=180∘−2KAF^+180∘−2KDH^=360∘−2(KAF^+KDH^)=360∘−2(180∘−ACD^)=360∘−2(180∘−60∘)=120∘
Mà FKH^=180∘−AKF^−HKD^=60∘
Vậy △KFH đều
b) Chứng minh như câu a, ta được △KEH đều, suy ra KEHF là hình thoi. Như vậy thì 2 đường chéo vuông góc, hay
17 tháng 12 2023
a: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
\(\widehat{EAD}=\widehat{FAD}\)
Do đó: ΔAED=ΔAFD
b: Xét ΔABC có
AD là đường trung tuyến
AD là đường phân giác
Do đó: ΔABC cân tại A
25 tháng 12 2021
a, xet tam giac ABD va tam giac ACD co : AD chung
AB = AC do tam giac ABC can tai A (gt)
goc BAD = goc CAD do AD la phan giac cua goc A (gt)
=> tam giac ABD = tam giac ACD (c - g - c)
=> BD = CD (dn)
xet tam giac BED va tam giac CFD co : goc BED = goc CFD = 90 do ...
goc B = goc C do tam giac ABC can tai A(gt)
=> tam giac BED = tam giac CFD (ch - gn)
=> DE = DF (dn)
b, cm o cau a
c, tam giac ABD = tam giac ACD (cau a)
=> goc ADC = goc ADB (dn)
goc ADC + goc ADB = 180 (kb)
=> goc ADC = 90
co DB = DC (cau a)
=> AD la trung truc cua BC (dn)
CH
Cô Hoàng Huyền
Admin
VIP
16 tháng 4 2018
1.
Xét tam giác vuông AHE có FI là đường trung tuyến ứng với cạnh huyền nên IF = IH = IA = AH/2 = 6 : 2 = 3 (cm)
Do IF = IH nên tam giác IHF cân tại I. Vậy thì \(\widehat{IFH}=\widehat{IHF}\)
Lại có \(\widehat{IHF}=\widehat{BHE}\) nên \(\widehat{IFH}=\widehat{BHE}\) (1)
Xét tam giác vuông BFC có FK là đường cao đồng thời là trung tuyến nên KF = KC = KB = BC : 2 = 4 (cm)
Ta cũng có KF = KB nên \(\widehat{HFK}=\widehat{HBK}\) (2)
Ta có \(\widehat{HBE}+\widehat{BHE}=90^o\) (3)
Từ (1), (2), (3) suy ra \(\widehat{IFH}+\widehat{HFK}=90^o\Rightarrow\widehat{IFK}=90^o\)
Xét tam giác vuông IFK, áp dụng định lý Pi-ta-go ta có:
IK2 = IF2 + FK2 = 32 + 42 = 25
\(\Rightarrow IK=5cm.\)
CH
Cô Hoàng Huyền
Admin
VIP
16 tháng 4 2018
2.
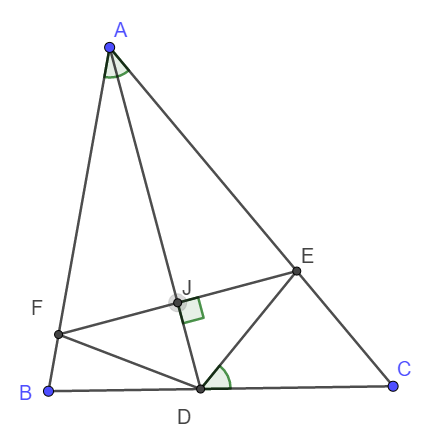
Gọi J là giao điểm của AD và EF.
Xét tam giác AFE có AJ là phân giác đồng thời đường cao nên AFE là tam giác cân tại A.
Vậy nên AJ đồng thời là trung trực của EF.
Lại có D thuộc AJ nên DE = DF. (1)
Xét tam giác AFD và tam giác AED có:
AF = AE
Cạnh AD chung
DF = DE
\(\Rightarrow\Delta AFD=\Delta AED\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFD}=\widehat{AED}\Rightarrow\widehat{BFD}=\widehat{DEC}\)
Lại có \(\widehat{FBD}=180^o-\widehat{BAC}-\widehat{BCA}\)
\(\widehat{DEC}=180^o-\widehat{EDC}-\widehat{CBA}=180^o-\widehat{BAC}-\widehat{BCA}\)
Vậy nên \(\widehat{DBF}=\widehat{DFB}\) hay tam giác DBF cân tại D.
Suy ra DF = DB. (2)
Từ (1) và (2) suy ra DB = DF = DE.
15 tháng 11 2019
Tham khảo
Câu hỏi của Hot girl 2k5 - Toán lớp 7 - Học toán với OnlineMath
15 tháng 11 2019
mik ko hieu cau c cho lam, ai giang giup mik cau c voi :((
a)Xét \(\Delta\)vuông AED và \(\Delta\)vuông AFD có
AED = AFD (do AD là phân giác góc A)
AD chung
=> \(\Delta\)AED = \(\Delta\)AFD (cạnh huyền- góc nhọn)
=> DE = DF (2 cạnh tương ứng)
b) Xét \(\Delta\)ABC có:
D là trung điểm BC => AD là đường trung tuyến của tam giác ABC
mà AD là phân giác của A
=> \(\Delta\)ABC cân tại A
=> B = C (đpcm)