Question

[Nguyễn Thị Thủy]

Cho tam giác ABC vuông tại A (AB>AC) có đường cao AH và E là trung điểm cạnh AB. Điểm K di động trên tia AC, KE cắt BC tại G. Hai đường thẳng KH và AG cắt nhau ở Q. CMR: Điểm Q luôn chạy trên 1 đường cố định khi K thay đổi ?

Answer 1

[Nguyễn Tất Đạt]

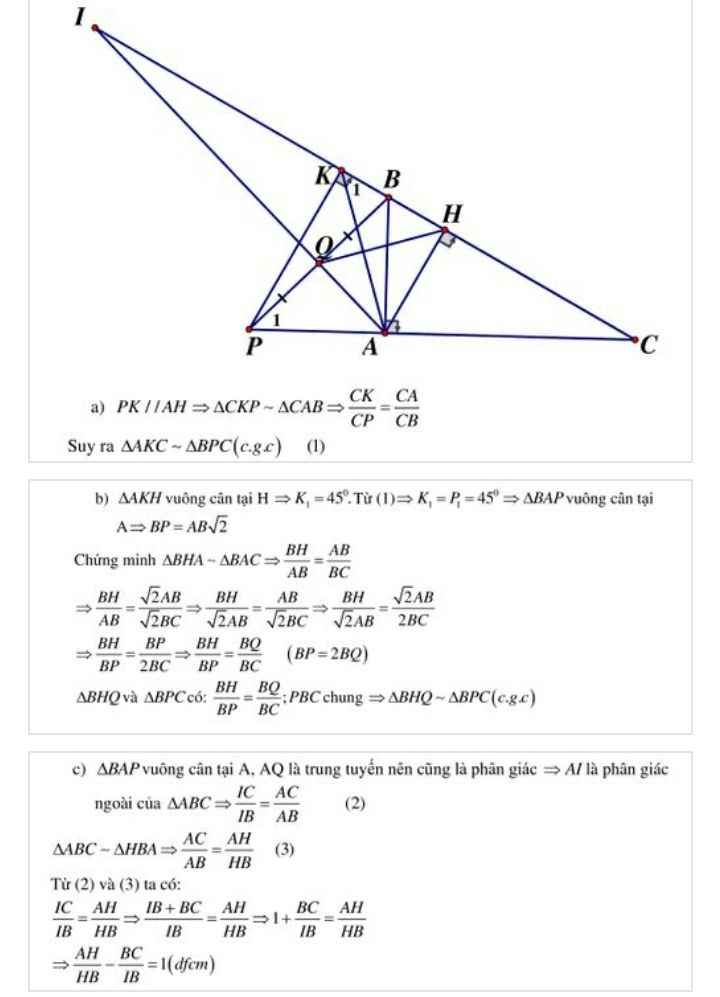
Gọi I là giao điểm của CQ và AH, F là giao của BK và AG.

Áp dụng ĐL Céva cho \(\Delta\)AKB: \(\frac{CK}{CA}.\frac{EA}{EB}.\frac{FB}{FK}=1\). Mà \(\frac{EA}{EB}=1\) nên \(\frac{CK}{CA}=\frac{FK}{FB}\)

=> CF // AB (ĐL Thales đảo). Do AB vuông góc AC nên CF vuông góc AC    (1)

Áp dụng ĐL Mélelaus cho \(\Delta\)CKQ với bộ điểm (H I A) thẳng hàng: \(\frac{HQ}{HK}.\frac{IC}{IQ}.\frac{AK}{AC}=1\)

Tương tự với \(\Delta\)FKQ: \(\frac{HQ}{HK}.\frac{GF}{GQ}.\frac{BK}{BF}=1\)

Từ đó: \(\frac{HQ}{HK}.\frac{IC}{IQ}.\frac{AK}{AC}=\frac{HQ}{HK}.\frac{GF}{GQ}.\frac{BK}{BF}\). Mà \(\frac{AK}{AC}=\frac{BK}{BF}\)(ĐL Thales)

Nên \(\frac{IC}{IQ}=\frac{GF}{GQ}\). Áp dụng ĐL Thales đảo cho \(\Delta\)CQF, suy ra: GI // CF (2)

Từ (1) và (2) suy ra: GI vuông góc AC. Do đó: I là trực tâm của \(\Delta\)ACG => CI vuông góc AG

Hay ^AQC = 90⁰ => Q nằm trên đường tròn đường kính AC cố định (đpcm).