Parabol y=x2+1 chia hình tròn có tâm tại gốc tọa độ, bán kính √5 thành hai phần. Tính tỉ số diện tích của hai phần này ( kết quả làm tròn tới hàng phần trăm)
A. 1,82
B. 1,78
C. 8,51
D. 8,50
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

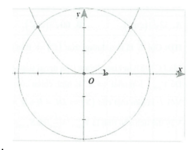

Diện tích phần giới hạn giữa đường tròn và parabol là:
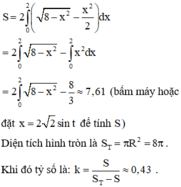
Chọn A.

diện tích hình tròn thứ 1 là
8 x 8 x 3,14 = 200,96cm2
bán kính hình tròn thứ 2 là
8 : 2 = 4cm
diện tích hình tròn thứ 2 là
4 x 4 x 3,14 = 50,24cm2
tỉ số % giữa diện tích hình tròn thứ 2 và thứ 1 là
50,24 : 200,96 = 0,25% = 25%
A)Diện tich hình 1 :200,96cm2
Diện tích hình 2 :50,24cm2
B)25%
Phương trình đường tròn: \(x^2+y^2=5\)
Phương trình tọa độ giao điểm: \(\left\{{}\begin{matrix}x^2=y-1\Rightarrow y\ge1\\x^2+y^2-5=0\end{matrix}\right.\)
\(\Rightarrow y^2+y-6=0\Rightarrow\left\{{}\begin{matrix}y=2\Rightarrow x=\pm1\\y=-3< 1\left(l\right)\end{matrix}\right.\)
Gọi \(S_1\) là phần diện tích phía trên, \(S_2\) là phần diện tích phía dưới và S là diện tích hình tròn
\(S=\pi R^2=5\pi\)
\(S_1=\int\limits^1_{-1}\left(\sqrt{5-x^2}-\left(x^2+1\right)\right)dx=\int\limits^1_{-1}\sqrt{5-x^2}dx-\dfrac{8}{3}=I-\dfrac{8}{3}\)
Đặt \(x=\sqrt{5}sint\Rightarrow dx=\sqrt{5}cost.dt\) ; \(\left\{{}\begin{matrix}x=-1\Rightarrow t=arcsin\dfrac{-1}{\sqrt{5}}\\x=1\Rightarrow t=arcsin\dfrac{1}{\sqrt{5}}\end{matrix}\right.\)
\(I=\int\limits^{arcsin\dfrac{1}{\sqrt{5}}}_{arcsin\dfrac{-1}{\sqrt{5}}}5.cos^2t.dt=\dfrac{5}{2}\int\limits^{arcsin\dfrac{1}{\sqrt{5}}}_{arcsin\dfrac{-1}{\sqrt{5}}}\left(1+cos2t\right)dt=2+5arcsin\dfrac{1}{\sqrt{5}}\)
\(\Rightarrow S_1=I-\dfrac{8}{3}=-\dfrac{2}{3}+5arcsin\dfrac{1}{\sqrt{5}}\)
\(\Rightarrow S_2=S-S_1=5\pi+\dfrac{2}{3}-5arcsin\dfrac{1}{\sqrt{5}}\)
\(\Rightarrow\dfrac{S_2}{S_1}=\dfrac{5\pi+\dfrac{2}{3}-5arcsin\dfrac{1}{\sqrt{5}}}{-\dfrac{2}{3}+5arcsin\dfrac{1}{\sqrt{5}}}\approx8.51\)