Question

[Nguyễn Hoài]

Parabol y=x²+1 chia hình tròn có tâm tại gốc tọa độ, bán kính √5 thành hai phần. Tính tỉ số diện tích của hai phần này ( kết quả làm tròn tới hàng phần trăm)

A. 1,82

B. 1,78

C. 8,51

D. 8,50

Answer 1

[Nguyễn Việt Lâm]

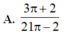
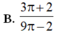
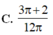
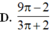
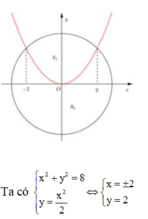
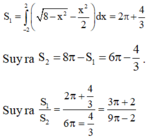
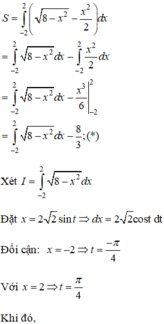
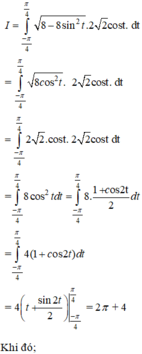
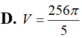
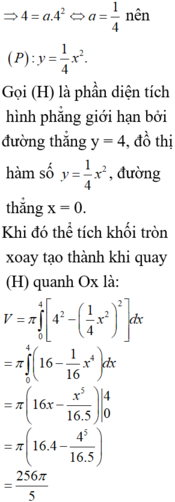
Phương trình đường tròn: \(x^2+y^2=5\)

Phương trình tọa độ giao điểm: \(\left\{{}\begin{matrix}x^2=y-1\Rightarrow y\ge1\\x^2+y^2-5=0\end{matrix}\right.\)

\(\Rightarrow y^2+y-6=0\Rightarrow\left\{{}\begin{matrix}y=2\Rightarrow x=\pm1\\y=-3< 1\left(l\right)\end{matrix}\right.\)

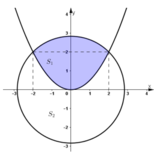
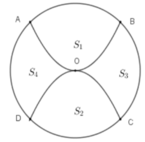
Gọi \(S_1\) là phần diện tích phía trên, \(S_2\) là phần diện tích phía dưới và S là diện tích hình tròn

\(S=\pi R^2=5\pi\)

\(S_1=\int\limits^1_{-1}\left(\sqrt{5-x^2}-\left(x^2+1\right)\right)dx=\int\limits^1_{-1}\sqrt{5-x^2}dx-\dfrac{8}{3}=I-\dfrac{8}{3}\)

Đặt \(x=\sqrt{5}sint\Rightarrow dx=\sqrt{5}cost.dt\) ; \(\left\{{}\begin{matrix}x=-1\Rightarrow t=arcsin\dfrac{-1}{\sqrt{5}}\\x=1\Rightarrow t=arcsin\dfrac{1}{\sqrt{5}}\end{matrix}\right.\)

\(I=\int\limits^{arcsin\dfrac{1}{\sqrt{5}}}_{arcsin\dfrac{-1}{\sqrt{5}}}5.cos^2t.dt=\dfrac{5}{2}\int\limits^{arcsin\dfrac{1}{\sqrt{5}}}_{arcsin\dfrac{-1}{\sqrt{5}}}\left(1+cos2t\right)dt=2+5arcsin\dfrac{1}{\sqrt{5}}\)

\(\Rightarrow S_1=I-\dfrac{8}{3}=-\dfrac{2}{3}+5arcsin\dfrac{1}{\sqrt{5}}\)

\(\Rightarrow S_2=S-S_1=5\pi+\dfrac{2}{3}-5arcsin\dfrac{1}{\sqrt{5}}\)

\(\Rightarrow\dfrac{S_2}{S_1}=\dfrac{5\pi+\dfrac{2}{3}-5arcsin\dfrac{1}{\sqrt{5}}}{-\dfrac{2}{3}+5arcsin\dfrac{1}{\sqrt{5}}}\approx8.51\)