Tìm số nguyên x sao cho P= 2x+3/x-1 có giá trị nguyên lớn nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 4 2023
A = \(\dfrac{2x-1}{x+2}\)
a, A là phân số ⇔ \(x\) + 2 # 0 ⇒ \(x\) # -2
b, Để A là một số nguyên thì 2\(x-1\) ⋮ \(x\) + 2
⇒ 2\(x\) + 4 - 5 ⋮ \(x\) + 2
⇒ 2(\(x\) + 2) - 5 ⋮ \(x\) + 2
⇒ 5 ⋮ \(x\) + 2
⇒ \(x\) + 2 \(\in\) { -5; -1; 1; 5}
⇒ \(x\) \(\in\) { -7; -3; -1; 3}
c, A = \(\dfrac{2x-1}{x+2}\)
A = 2 - \(\dfrac{5}{x+2}\)
Với \(x\) \(\in\) Z và \(x\) < -3 ta có
\(x\) + 2 < - 3 + 2 = -1
⇒ \(\dfrac{5}{x+2}\) > \(\dfrac{5}{-1}\) = -5 ⇒ - \(\dfrac{5}{x+2}\)< 5
⇒ 2 - \(\dfrac{5}{x+2}\) < 2 + 5 = 7 ⇒ A < 7 (1)
Với \(x\) > -3; \(x\) # - 2; \(x\in\) Z ⇒ \(x\) ≥ -1 ⇒ \(x\) + 2 ≥ -1 + 2 = 1
\(\dfrac{5}{x+2}\) > 0 ⇒ - \(\dfrac{5}{x+2}\) < 0 ⇒ 2 - \(\dfrac{5}{x+2}\) < 2 (2)
Với \(x=-3\) ⇒ A = 2 - \(\dfrac{5}{-3+2}\) = 7 (3)
Kết hợp (1); (2) và(3) ta có A(max) = 7 ⇔ \(x\) = -3
6 tháng 11 2016
bài 2
Ta có:
\(A=\left|x-102\right|+\left|2-x\right|\Rightarrow A\ge\left|x-102+2-x\right|=-100\Rightarrow GTNNcủaAlà-100\)đạt được khi \(\left|x-102\right|.\left|2-x\right|=0\)
Trường hợp 1: \(x-102>0\Rightarrow x>102\)
\(2-x>0\Rightarrow x< 2\)
\(\Rightarrow102< x< 2\left(loại\right)\)
Trường hợp 2:\(x-102< 0\Rightarrow x< 102\)
\(2-x< 0\Rightarrow x>2\)
\(\Rightarrow2< x< 102\left(nhận\right)\)
Vậy GTNN của A là -100 đạt được khi 2<x<102.
T
28 tháng 11 2023
Giup mình với ah.
1- Tính :
A= 5. | x- 5 | - 3x + 1
2 - Tìm các số nguyên x,y ; sao cho :
a) 5/x - y/3 = 1/6 b) 5/x + y/4 = 1/8
3- Tìm giá trị lớn nhất của Q = 27-2x/12-x ( x là số nguyên)
---------------------------------------------------------------------------------------------
3 tháng 5 2019
a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
4 tháng 5 2019
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
HP
22 tháng 3 2021
b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)
KT
1
KN
14 tháng 4 2019
\(A=\frac{2x-1}{x-3}=\frac{2\left(x-3\right)+5}{x-3}=2+\frac{5}{x-3}\)
Để Amax thì \(\frac{5}{x-3}\) đạt GTLN
\(\Leftrightarrow x-3=1\)
\(\Leftrightarrow x=1+3\)
\(\Leftrightarrow x=4\)
Vậy Amax\(\Leftrightarrow x=4\)
ND
Nguyễn Đức Trí
VIP
28 tháng 11 2023
1) \(A=5.\left|x-5\right|-3x+1\)
\(A=\left[{}\begin{matrix}5.\left(x-5\right)-3x+1\left(x-5\ge0\right)\\5.\left(5-x\right)-3x+1\left(x-5< 0\right)\end{matrix}\right.\)
\(A=\left[{}\begin{matrix}5x-25-3x+1\left(x\ge5\right)\\25-5x-3x+1\left(x< 5\right)\end{matrix}\right.\)
\(A=\left[{}\begin{matrix}2x-24\left(x\ge5\right)\\26-8x\left(x< 5\right)\end{matrix}\right.\)
29 tháng 11 2023
3:
\(Q=\dfrac{27-2x}{12-x}=\dfrac{2x-27}{x-12}\)
\(\Leftrightarrow Q=\dfrac{2x-24-3}{x-12}=2-\dfrac{3}{x-12}\)
Để Q lớn nhất thì \(2-\dfrac{3}{x-12}\) lớn nhất
=>\(\dfrac{3}{x-12}\) nhỏ nhất
=>x-12 là số nguyên âm lớn nhất
=>x-12=-1
=>x=11
Vậy: \(Q_{min}=2-\dfrac{3}{11-12}=2+3=5\) khi x=11
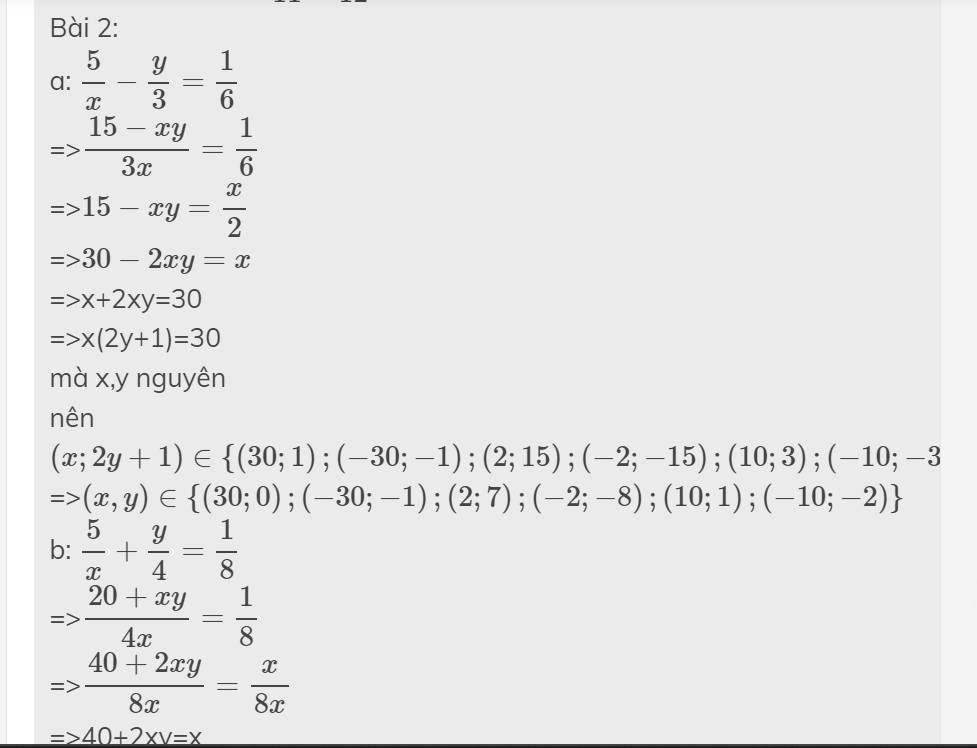
Bài 2:
a: \(\dfrac{5}{x}-\dfrac{y}{3}=\dfrac{1}{6}\)
=>\(\dfrac{15-xy}{3x}=\dfrac{1}{6}\)
=>\(15-xy=\dfrac{x}{2}\)
=>\(30-2xy=x\)
=>x+2xy=30
=>x(2y+1)=30
mà x,y nguyên
nên \(\left(x;2y+1\right)\in\left\{\left(30;1\right);\left(-30;-1\right);\left(2;15\right);\left(-2;-15\right);\left(10;3\right);\left(-10;-3\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(30;0\right);\left(-30;-1\right);\left(2;7\right);\left(-2;-8\right);\left(10;1\right);\left(-10;-2\right)\right\}\)
b: \(\dfrac{5}{x}+\dfrac{y}{4}=\dfrac{1}{8}\)
=>\(\dfrac{20+xy}{4x}=\dfrac{1}{8}\)
=>\(\dfrac{40+2xy}{8x}=\dfrac{x}{8x}\)
=>40+2xy=x
=>x-2xy=40
=>x(1-2y)=40
mà x,y nguyên
nên \(\left(x;1-2y\right)\in\left\{\left(40;1\right);\left(-40;-1\right);\left(8;5\right);\left(-8;-5\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(40;0\right);\left(-40;1\right);\left(8;-2\right);\left(-8;3\right)\right\}\)
ND
Nguyễn Đức Trí
VIP
11 tháng 7 2023
a) \(A=\dfrac{3}{x-1}\)
Điều kiện \(|x-1|\ge0\)
\(\Rightarrow A=\dfrac{3}{x-1}\ge0\)
\(GTNN\left(A\right)=0\) \(\Rightarrow x-1=+\infty\Rightarrow x\rightarrow+\infty\)
b) \(GTLN\left(A\right)\) không có \(\left(A=\dfrac{3}{x-1}\ge0\right)\)
Theo đề ra, ta có:
\(x\in Z\Rightarrow2x+3;x-1\in Z\)
Mà: \(P\in Z\Rightarrow\dfrac{2x+3}{x-1}\in Z\Rightarrow2x+3⋮x-1\Rightarrow2x-2+5⋮x-1\Rightarrow2\left(x-1\right)+5⋮x-1\)
\(\Rightarrow5⋮x-1\Rightarrow x-1\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\Rightarrow x\in\left\{2;6;0;-4\right\}\)
\(\Rightarrow\dfrac{2x+3}{x-1}\in\left\{7;\pm3;1\right\}\Rightarrow P\in\left\{7;\pm3;1\right\}\)
Vậy giá trị lớn nhất của \(P=7\) khi \(x=2\)