trong các hình bình hành ngoại tiếp đường tròn (O;r), hãy tìm hình bình hành có diện tích lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 6 2018
Gọi BD ∩ AC=I
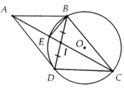
Ta có B A I ^ = A C D ^ = E B D ^ = 1 2 s đ E D ⏜
Áp dụng bổ đề Þ ĐPCM
12 tháng 9 2023
a: góc AHE+góc EAH=90 độ
góc ACB+góc EAH=90 độ
Do đó: góc AHE=góc ACB=1/2*sđ cung AB
=>góc BHM=1/2*sđ cung AB
=>góc BHM=góc BMH
=>ΔBMH cân tại B
mà BC là đường cao
nên BC là trung trực của HM
b: Xét (O) có
ΔABI nội tiếp
AI là đường kính
Do đó: ΔABI vuông tại B
=>BI vuông góc AB
=>BI//CH
Xét (O) có
ΔACI nội tiếp
AI là đường kính
Do đó: ΔACI vuông tại C
=>CI vuông góc AC
=>CI//BH
Xét tứ giác BHCI có
BH//CI
BI//CH
=>BHCI là hình bình hành
CM
6 tháng 11 2017
.
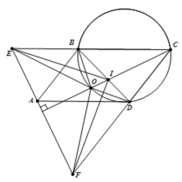
3). Theo trên, ta có B E = C D mà C E = C F ⇒ B C = D F .
Ta có CI là đường phân giác góc BCD, nên I B I D = C B C D = D F B E ⇒ I B . B E = I D . D F .
Mà CO là trung trực EF và I ∈ C O , suy ra IE=IF.
Từ hai đẳng thức trên, suy ra I B . B E . E I = I D . D F . F I .
CM
23 tháng 1 2018
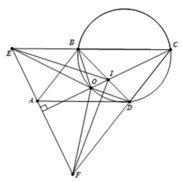
2). Từ Δ O B E = Δ O D C ⇒ O E = O C .
Mà CO là đường cao tam giác cân CEF , suy ra OE=OF.
Từ đó O E = O C = O F , vậy O là tâm đường tròn ngoại tiếp tam giác .
A B C D M N Q P H O
Xét hình bình hành ABCD ngoại tiếp (O)
Theo đầu bài ta suy ra các cạnh của hình bình hành là tiếp tuyến của (O)
Gọi M , N , P , Q là các tiếp điểm của đường tròn với các cạnh như hình vẽ
Theo tính chất tiếp tuyến có: CM = CN ; AP = AQ ; BM = BQ ; PD = DN
=> CM + BM + AP + PD = CN + DN + AQ + BQ
=> 2BC = 2AB
=> BC = AB
Kẻ AH \(\perp\)BC ta có: AB > AH (Đường xiên , hình chiếu)
Dấu "=" xảy ra khi ^ABC = 90o
Ta có : OM ⊥ BC ; OP ⊥ AD , AD // BC
=> P , O , M thẳng hàng
Do đó AH = PM = 2r
\(S_{ABCD}=AH.BC=2r.AB\ge2r.AH=2r.2r=4r^2\)
Dấu "=" xảy ra \(\Leftrightarrow AH\equiv AB\Leftrightarrow\widehat{ABC}=90^o\)
Mà ABCD là hình bình hành
=> ABCD là hình vuông
Vậy trong các hình bình hành ngoại tiếp đường tròn (O;r) thì hình vuông có diện tích nhỏ nhất và bằng 4r2
hình đâu bn
ko có hình sao biết đc!!