Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

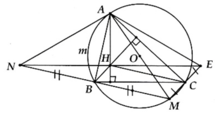
a, BH ^ AC và CM ^ AC Þ BH//CM
Tương tự => CH//BM
=> BHCM là hình bình hành
b, Chứng minh BNHC là hình bình hành
=> NH//BC
=> AH ^ NH => A H M ^ = 90 0
Mà A B N ^ = 90 0 => Tứ giác AHBN nội tiếp
c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng
d, A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN
AN = AM = 2R, AB = R 3 => A m B ⏜ = 120 0
S A O B = 1 2 S A B M = R 2 3 4
S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3
=> S cần tìm = 2 S A m B ⏜ = R 2 6 4 π - 3 3
A B C D M N Q P H O
Xét hình bình hành ABCD ngoại tiếp (O)
Theo đầu bài ta suy ra các cạnh của hình bình hành là tiếp tuyến của (O)
Gọi M , N , P , Q là các tiếp điểm của đường tròn với các cạnh như hình vẽ
Theo tính chất tiếp tuyến có: CM = CN ; AP = AQ ; BM = BQ ; PD = DN
=> CM + BM + AP + PD = CN + DN + AQ + BQ
=> 2BC = 2AB
=> BC = AB
Kẻ AH \(\perp\)BC ta có: AB > AH (Đường xiên , hình chiếu)
Dấu "=" xảy ra khi ^ABC = 90o
Ta có : OM ⊥ BC ; OP ⊥ AD , AD // BC
=> P , O , M thẳng hàng
Do đó AH = PM = 2r
\(S_{ABCD}=AH.BC=2r.AB\ge2r.AH=2r.2r=4r^2\)
Dấu "=" xảy ra \(\Leftrightarrow AH\equiv AB\Leftrightarrow\widehat{ABC}=90^o\)
Mà ABCD là hình bình hành
=> ABCD là hình vuông
Vậy trong các hình bình hành ngoại tiếp đường tròn (O;r) thì hình vuông có diện tích nhỏ nhất và bằng 4r2
hình đâu bn
ko có hình sao biết đc!!