Tam giác ABC cân tại A. Kẻ BD vuông góc với AC, CE vuông góc với AB. Gọi O là giao điểm BD và CE. Chứng minh:
a/ AO là phân giác của góc BAC.
b/ Vẽ tia Bx vuông góc với AB tại điểm B và Cy vuông góc với AC tại điểm C, Bx cắt Cy tại K. CM: HB=HC và AH là đường trung trực của đoạn BC.
(Vẽ hình luôn nha!!!)
*Thank...
Đọc tiếp
Tam giác ABC cân tại A. Kẻ BD vuông góc với AC, CE vuông góc với AB. Gọi O là giao điểm BD và CE. Chứng minh:
a/ AO là phân giác của góc BAC.
b/ Vẽ tia Bx vuông góc với AB tại điểm B và Cy vuông góc với AC tại điểm C, Bx cắt Cy tại K. CM: HB=HC và AH là đường trung trực của đoạn BC.
(Vẽ hình luôn nha!!!)
*Thank you*
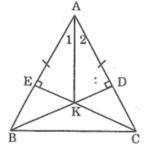
Sửa đề: Bx cắt Cy tại H
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc BAD chung
Do đó: ΔADB=ΔAEC
=>AD=AE
Xét ΔEAO vuông tại E và ΔDAO vuông tại D có
AO chung
AD=AE
Do đo: ΔEAO=ΔDAO
=>góc EAO=góc DAO
=>AO là phân giác của góc BAC
b: Xét ΔABH vuông tại B và ΔACH vuông tại C có
AH chung
AB=AC
Do đo: ΔABH=ΔACH
=>BH=CH
mà AB=AC
nên AH là trung trực của BC